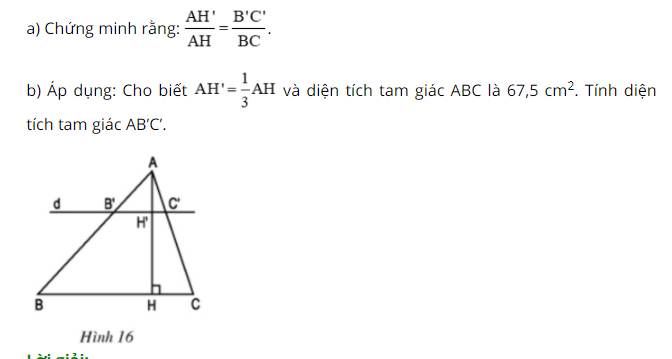
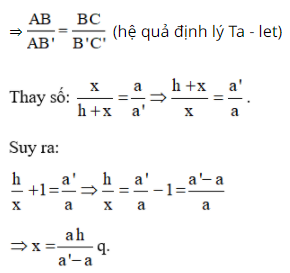Bài 10, 11, 12, 13, 14 trang 63, 64 SGK Toán 8 tập 2 - Luyện tập

Bài 10 trang 63 SGK Toán lớp 8 tập 2

Câu hỏi:

\(∆ABC\) có đường cao \(AH\). Đường thẳng \(d\) song song với \(BC\), cắt các cạnh \(AB, AC\) và đường cao \(AH\) theo thứ tự tại các điểm \(B', C'\) và \(H'\)(h.16)

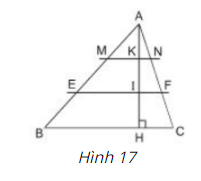
Lời giải:

a. Vì \(B'C' // BC\) \( \Rightarrow \dfrac{B'C'}{BC} = \dfrac{AB'}{AB}\)   (1) (theo hệ quả định lý TaLet)

Trong \(∆ABH\) có \(B'H' // BH\) \( \Rightarrow \dfrac{AH'}{AH} = \dfrac{AB'}{AB}\)  (2) (theo hệ quả định lý TaLet)

Từ (1) và (2) \( \Rightarrow \dfrac{B'C'}{BC} = \dfrac{AH'}{AH}\)

b.  \(B'C' // BC\) mà \(AH ⊥ BC\) nên \(AH' ⊥ B'C'\) hay \(AH'\) là đường cao của \(∆AB'C'\).

 Giả thiết: \(AH' = \dfrac{1}{3} AH\).

Áp dụng kết quả câu a) ta có:

\(\dfrac{B'C'}{BC}= \dfrac{AH'}{AH} = \dfrac{1}{3}\) 

\(\Rightarrow  B'C' = \dfrac{1}{3} BC\)

\(\eqalign{
& {S_{AB'C'}} = {1 \over 2}AH'.B'C' \cr&\;\;\;\;\;\;\;\;\;\;\;= {1 \over 2}.{1 \over 3}AH.{1 \over 3}BC \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;= {1 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;= {1 \over 9}.{S_{ABC}}\cr&\;\;\;\;\;\;\;\;\;\;\; = {1 \over 9}.67,5 = 7,5\,\,c{m^2} \cr} \)

Bài 11 trang 63 SGK Toán lớp 8 tập 2

Câu hỏi:

Tam giác ABC có BC = 15cm. Trên đường cao AH lấy các điểm I, K sao cho AK = KI = IH. Qua I và K vẽ các đường EF // BC, MN // BC (h.17).

a) Tính độ dài các đoạn thẳng MN và EF.

b) Tính diện tích tứ giác MNFE, biết rằng diện tích của tam giác ABC là 270cm2.

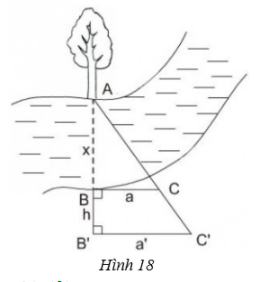
Lời giải:

a. 

\(∆ABC\) có \(MN // BC\) (gt)

\( \Rightarrow \dfrac{MN}{CB} = \dfrac{AK}{AH}\) (kết quả bài tập 10) (định lý TaLet)

Mà \(AK = KI = IH\).

Nên \(\dfrac{AK}{AH} = \dfrac{1}{3}\) 

\( \Rightarrow \dfrac{MN}{CB} = \dfrac{1}{3}\) 

\( \Rightarrow  MN = \dfrac{1}{3}BC = \dfrac{1}{3}.15 = 5\, cm\).

\(∆ABC\) có \(EF // BC\) (gt)

\( \Rightarrow \dfrac{EF}{BC} = \dfrac{AI}{AH} = \dfrac{2}{3}\) (định lý TaLet)

\(\Rightarrow  EF =\dfrac{2}{3}.BC= \dfrac{2}{3}.15 =10 \,cm\).

b. 

Theo câu a) ta có: \(AK=\dfrac{1}{3}AH;MN=\dfrac{1}{3}BC;\) \(AI=\dfrac{2}{3}AH;EF=\dfrac{2}{3}BC\)

Nên:

\(\eqalign{
& {S_{AMN}} = {1 \over 2}.AK.MN \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}.{1 \over 3}AH.{1 \over 3}BC \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 9}.{S_{ABC}} \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 9}.270 = 30\,c{m^2} \cr} \)

\(\eqalign{
& {S_{AEF}} = {1 \over 2}.AI.EF \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over 2}.{2 \over 3}AH.{2 \over 3}BC \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {4 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {4 \over 9}.{S_{ABC}} \cr 
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {4 \over 9}.270 = 120\,c{m^2} \cr} \)

Do đó \({S_{MNFE}} = {S_{AEF}} - {S_{AMN}} = 120 - 30 \)\(\,= 90c{m^2}\)

Bài 12 trang 64 SGK Toán lớp 8 tập 2

Câu hỏi:

Có thể đo chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không?

Người ta tiến hành đo đạc các hệ yếu tố cần thiết để làm theo chiều rộng của dòng sông mà không cần phải sang bờ bên kia (h18). Nhìn hình vẽ, hãy mô tả những công việc cần làm và tính khoảng cách \ (AB = x \) theo \ (BC = a, B'C '= a', BB '= h \).

Phương pháp:

Áp dụng: Hệ quả của TaLet định nghĩa.

Lời giải:

+ Mô tả cách làm:

- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.

- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.

- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.

+ Cách tính AB.

Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’

ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)

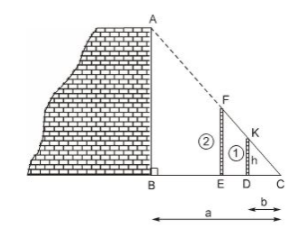
Bài 13 trang 64 SGK Toán lớp 8 tập 2

Câu hỏi:

Có thể đo gián tiếp chiều cao của một bức tường khá cao bằng dụng cụ đơn giản được không?

Hình 19 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: Hai cọc thẳng đứng (cọc 1 cố định; cọc 2 có thể di động được) và sợi dây FC. Cọc 1 có chiều cao DK = h. Các khoảng cách BC = a, DC = b đo được bằng thước dây thông dụng.

a) Em hãy cho biết người ta tiến hành đo đạc như thế nào.

b) Tính chiều cao AB theo h, a, b.

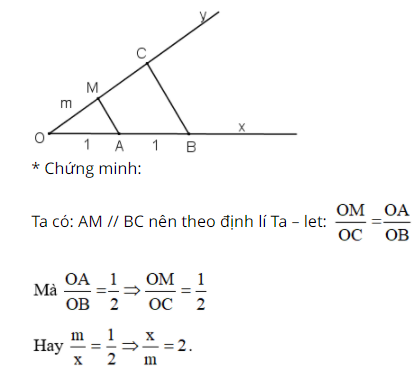
Lời giải:

a) Cách tiến hành:

- Đặt hai cọc thẳng đứng, di chuyển cọc \(2\) sao cho \(3\) điểm \(A,F,K\) nằm trên một đường thẳng.

- Dùng sợi dây căng thẳng qua \(2\) điểm \(F\) và \(K\) để xác định điểm \(C\) trên mặt đất (\(3\) điểm \(F,K,C\) thẳng hàng).

b) \(∆ABC\) có \(AB // DK\) nên \(\dfrac{DK}{AB} = \dfrac{DC}{BC}\) 

\( \Rightarrow  AB = \dfrac{DK.BC}{DC} = \dfrac{h.a}{b}\) (theo hệ quả định lí Talet)

Vậy chiều cao của bức tường \( AB = \dfrac{h.a}{b}\).

Bài 14 trang 64 SGK Toán lớp 8 tập 2

Câu hỏi:

Cho ba đoạn thẳng có độ dài là m, n, p (cùng đơn vị đo).

Dựng đoạn thẳng có độ dài \(x\) sao cho:

a. \(\dfrac{x}{m} =2\); b. \(\dfrac{x}{n}= \dfrac{2}{3}\); c. \(\dfrac{m}{x} = \dfrac{n}{p}\)

Phương pháp:

Áp dụng hệ quả của định lý TaLet.

Lời giải:

a)

- Cách dựng:

   + Vẽ hai tia Ox, Oy không đối nhau.

   + Trên tia Ox lấy A và B sao cho OA = 1 đơn vị, OB = 2 đơn vị.

   + Trên tia Oy lấy điểm M sao cho OM = m.

   + Vẽ đường thẳng qua B và song song với MA cắt Oy tại C.

Khi đó đoạn thẳng OC chính là đoạn thẳng cần dựng.

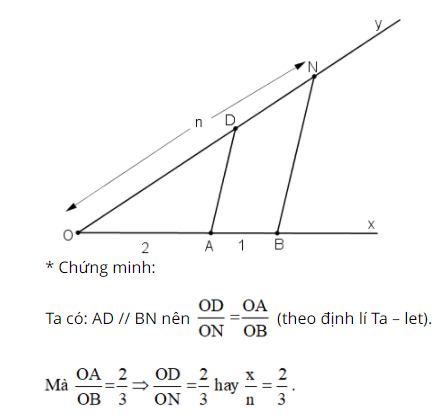
b) Cách dựng:

   + Vẽ hai tia Ox, Oy không đối nhau.

   + Trên tia Ox lấy A và B sao cho OA = 2 đơn vị, OB = 3 đơn vị

   + Trên tia Oy lấy điểm N sao cho ON = n.

   + Vẽ đường thẳng qua A và song song với NB cắt Oy tại D.

Khi đó đoạn thẳng OD chính là đoạn thẳng cần dựng.

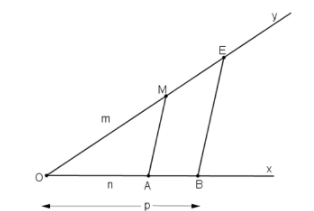
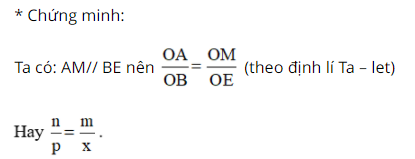
c) Cách dựng:

   + Vẽ hai tia Ox, Oy không đối nhau.

   + Trên tia Ox lấy A và B sao cho OA = n đơn vị, OB = p đơn vị

   + Trên tia Oy lấy điểm M sao cho OM = m

   + Vẽ đường thẳng qua B và song song với MA cắt Oy tại E

Khi đó đoạn thẳng OE chính là đoạn thẳng cần dựng.

Sachbaitap.com