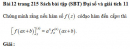Bài 10 trang 215 Sách bài tập (SBT) Đại số và giải tích 11

Cho hàm số

\(f\left( x \right) = {x^3} + b{x^2} + cx + d\) ;    (C)

\(g\left( x \right) = {x^2} - 3x - 1.\)

a) Xác định b, c, d sao cho đồ thị (C) đi qua các điểm \(\left( {1;3} \right),\left( { - 1; - 3} \right)\) và \(f'\left( {{1 \over 3}} \right) = {5 \over 3}\) ;

b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ \({x_0} = 1\) ;

c) Giải phương trình \(f'\left( {\sin t} \right) = 3\) ;

d) Giải phương trình \(f''\left( {\cos t} \right) = g'\left( {\sin t} \right)\) ;

e) Tìm giới hạn \(\mathop {\lim }\limits_{z \to 0} {{f''\left( {\sin 5z} \right) + 2} \over {g'\left( {\sin 3z} \right) + 3}}.\)

Giải :

a)

\(\eqalign{
& c = 2,b = - 1,d = 1 \cr
& \Rightarrow f\left( x \right) = {x^3} - {x^2} + 2x + 1{\rm{ }}; \cr} \)

b) \(f'\left( x \right) = 3{x^2} - 2x + 2 \Rightarrow f'\left( 1 \right) = 3.\)

Phương trình tiếp tuyến tại \(M\left( {1;3} \right)\) là

\(y - 3 = 3\left( {x - 1} \right)\) hay \(y = 3x.\)

c)

\(\eqalign{
& f'\left( {\sin t} \right) = 3{\sin ^2}t - 2\sin t + 2. \cr
& f'\left( {\sin t} \right) = 3 \cr
& \Leftrightarrow 3{\sin ^2}t - 2\sin t - 1 = 0 \cr
& \Leftrightarrow \left[ \matrix{
\sin t = 1 \hfill \cr
\sin t = - {1 \over 3} \hfill \cr} \right. \cr
& \Leftrightarrow \left[ \matrix{
t = {\pi \over 2} + k2\pi \hfill \cr
t = \arcsin \left( { - {1 \over 3}} \right) + k2\pi \hfill \cr
t = \pi - \arcsin \left( { - {1 \over 3}} \right) + k2\pi \hfill \cr} \right.\left( {k \in Z} \right). \cr} \)

d)

\(\eqalign{
& f''\left( x \right) = 6x - 2 \cr
& \Rightarrow f''\left( {\cos t} \right) = 6\cos t - 2 \cr} \) ;

\(\eqalign{
& g'\left( x \right) = 2x - 3 \cr
& \Rightarrow g'\left( {\sin t} \right) = 2\sin t - 3. \cr} \)

Vậy

\(\eqalign{
& 6\cos t - 2 = 2\sin t - 3 \cr
& \Leftrightarrow 2\sin t - 6\cos t = 1 \cr
& \Leftrightarrow \sin t - 3\cos t = {1 \over 2}. \cr} \)

Đặt \(\tan \varphi  = 3,\) ta được

\(\sin \left( {t - \varphi } \right) = {1 \over 2}\cos \varphi  = \alpha .\) Suy ra 

\(\left[ \matrix{
t = \varphi + \arcsin \alpha + k2\pi \hfill \cr
t = \pi + \varphi - \arcsin \alpha + k2\pi {\rm{ }}\left( {k \in Z} \right). \hfill \cr} \right.\)

e)

\(\mathop {\lim }\limits_{z \to 0} {{f''\left( {\sin 5z} \right) + 2} \over {g'\left( {\sin 3z} \right) + 3}} = \mathop {\lim }\limits_{z \to 0} {{6\sin 5z} \over {2\sin 3z}} = 5\mathop {\lim }\limits_{z \to 0} {{{{\sin 5z} \over {5z}}} \over {{{\sin 3z} \over {3z}}}} = 5.\)