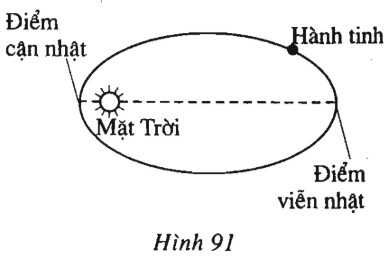
Bài 105 trang 122 SBT Hình học 10 Nâng cao

Các hành tinh và các sao chổi trong hệ Mặt Trời có quỹ đạo là các đường elip nhận tâm Mặt Trời làm một tiêu điểm. Điểm gần Mặt Trời nhất trên quỹ đạo gọi là điểm cận nhất. Điểm xa Mặt Trời nhất trên quỹ đạo gọi là điểm viễn nhật. Các điểm này là các đỉnh trên trục lớn của quỹ đạo (h.91).

a) Tìm tâm sai của quỹ đạo Trái Đất biết rằng tỉ số các khoảng cách từ điểm cận nhất đếnMặt Trời và từ điểm viễn nhất đến Mặt Trời là \( \dfrac{{59}}{{61}}\).

b) Tính khoảng cách từ Trái Đất đến Mặt Trời khi Trái Đất ở điểm cận nhất, ở điểm viễn nhất, biết rằng quỹ đạo có độ dài nửa trục lớn là \(93000000\) dặm.

Giải

a) Gọi \(m, n\) thứ tự là các khoảng cách từ điểm viễn nhật và điểm cận nhật đến Mặt Trời.

khi đó tâm sai của quỹ đạo Trái Đất là:

\(e =  \dfrac{{2c}}{{2a}} =  \dfrac{{(a + c) - (a - c)}}{{a + c + a - c}} \)

\(=  \dfrac{{m - n}}{{m + n}} =  \dfrac{{1 -  \dfrac{n}{m}}}{{1 +  \dfrac{n}{m}}}\)

\(=  \dfrac{{1 -  \dfrac{{59}}{{61}}}}{{1 +  \dfrac{{59}}{{61}}}} =  \dfrac{1}{{60}}\).

b) Theo câu a), ta có \(e =  \dfrac{1}{{60}} =  \dfrac{c}{a}  \)

\(  \Rightarrow  \dfrac{1}{{60}} =  \dfrac{c}{{93000000}}    \Rightarrow c = 1550000\).

Khoảng cách gần nhất giữa Trái Đất và Mặt Trời là:

\(a-c=91450000\) (dặm).

Khoảng cách xa nhất giữa Trái Đất và Mặt Trời là:

\(a+c=94550000\) (dặm).

Sachbaitap.com