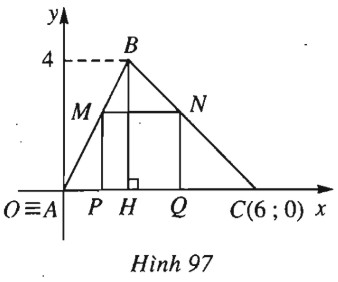
Bài 13 trang 101 SBT Hình học 10 Nâng cao

Cho tam giác \(ABC\) có \(A(0 ; 0),\) \( B(2 ; 4),\) \( C(6 ; 0)\) và các điểm \(M\) trên cạnh \(AB, N\) trên cạnh \(BC, P\) và \(Q\) trên cạnh \(AC\) sao cho \(MNPQ\) là hình vuông. Tìm tọa độ các điểm \(M, N, P, Q.\)

Giải

(h.97).

\(A(0 ; 0),  C(6 ; 0)    \Rightarrow  A, C \in  Ox \)

\(  \Rightarrow  P, Q  \in  Ox \)

\(   \Rightarrow   P = ({x_P} ; 0), Q = ({x_Q} ; 0)\) với \(0 < x_p < x_Q < 6.\)

Phương trình đường thẳng \(AB :y=2x;\)

Phương trình đường thẳng \(AC: y=0.\)

Gọi cạnh hình vuông là \(a\). Ta có

\( \dfrac{{MN}}{{AC}} =  \dfrac{{BM}}{{BA}}    \Rightarrow    \dfrac{a}{6} =  \dfrac{{BM}}{{BA}}\)    (1).

Kẻ \(BH \bot AC\), suy ra \(BH=4\). Ta có

\( \dfrac{{MP}}{{BH}} =  \dfrac{{AM}}{{AB}}   \Rightarrow    \dfrac{a}{4} =  \dfrac{{AM}}{{AB}} \)     (2).

Từ (1)  và (2) suy ra :\( \dfrac{a}{6} +  \dfrac{a}{4} =  \dfrac{{BM}}{{AB}} +  \dfrac{{AM}}{{AB}} = 1\). Do đó \(a =  \dfrac{{12}}{5}\).Vậy \({y_M} = {y_N} =  \dfrac{{12}}{5}\).

Do \(M \in AB\) nên \({y_M} = 2{x_M}\), suy ra \({x_M} =  \dfrac{6}{5}, {x_P} = {x_M} =  \dfrac{6}{5}\).

Vì \(PQ = {x_Q} - {x_P}\) nên \({x_Q} = {x_P} + a =  \dfrac{6}{5} +  \dfrac{{12}}{5} =  \dfrac{{18}}{5}\).

Các điểm cần tìm là \(M\left( { \dfrac{6}{5} ;  \dfrac{{12}}{5}} \right),  P\left( { \dfrac{6}{5} ; 0} \right), \) \( Q\left( { \dfrac{{18}}{5} ; 0} \right),  N\left( { \dfrac{{18}}{5} ;  \dfrac{{12}}{5}} \right)\).

Sachbaitap.com