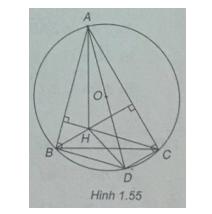
Bài 1.35 trang 34 Sách bài tập (SBT) Toán Hình học 10Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác, D là điểm đối xứng của A qua O. Cho tam giác ABC nội tiếp trong đường tròn tâm O, H là trực tâm của tam giác, D là điểm đối xứng của A qua O. a) Chứng minh tứ giác HCDB là hình bình hành. b) Chứng minh: \(\overrightarrow {HA} + \overrightarrow {HD} = 2\overrightarrow {HO} \); \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} \); \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} \). c) Gọi G là trọng tâm tam giác ABC. Chứng minh \(\overrightarrow {OH} = 3\overrightarrow {OG} \) Từ đó có kết luận gì về ba điểm O, H, G? Gợi ý làm bài (Xem h.1.55)
a) Vì AD là đường kính của đường tròn tâm O nên \(BD \bot AB,DC \bot AC\) Ta có \(CH \bot AB,BH \bot AC\) nên suy ra CH // BD và BH // DC. Vậy tứ giác HCDB là hình bình hành. b) Vì O là trung điểm của AD nên \(\overrightarrow {HA} + \overrightarrow {HD} = 2\overrightarrow {HO} (1)\) Vì tứ giác HCDB là hình bình hành nên ta có \(\overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HD} \). Vậy từ (1) suy ra: \(\overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = 2\overrightarrow {HO} (2)\) Theo quy tắc ba điểm, từ (2) suy ra \(\overrightarrow {HO} + \overrightarrow {OA} + \overrightarrow {HO} + \overrightarrow {OB} + \overrightarrow {HO} + \overrightarrow {OC} = 2\overrightarrow {HO} \) Vậy \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} (3)\) c) G là trọng tâm của tam giác ABC. Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \) Từ (3) suy ra \(\overrightarrow {OH} = 3\overrightarrow {OG} \) Vậy ba điểm O, H, G thẳng hàng. Trong một tam giác trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O thẳng hàng. Sachbaitap.net
Xem lời giải SGK - Toán 10 - Xem ngay >> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, (Xem ngay) Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, làm quen kiến thức, định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 10
Xem thêm tại đây:
Bài 3: Tích của vec tơ với một số
|
-

Bài 1.39 trang 43 Sách bài tập (SBT) Toán Hình học 10
Xét xem các cặp vec tơ sau có cùng phương không? Trong trường hợp cùng phương thì xét xem chúng cùng hướng hay ngược hướng.

 Tải ngay
Tải ngay