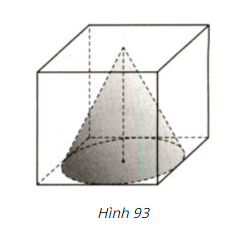
Bài 15, 16, 17, 18 trang 117 SGK Toán 9 tập 2 - Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt

Bài 15 trang 117 SGK Toán lớp 9 tập 2

Câu hỏi:

Một hình nón được đặt vào bên  trong của một hình lập phương như hình vẽ (cạnh của hình lập phương bằng \(1\)). Hãy tính:

a) Bán kính đáy của hình nón.

b) Độ dài đường sinh.

Lời giải:

a) Có đường tròn đáy của hình nón nội tiếp trong hình vuông là một mặt của hình lập phương. Do đó bán kính của đáy hình nón bằng một nửa cạnh hình lập phương và bằng \(r=0,5\).

b) Đỉnh của hình nón tiếp xúc với một mặt của hình lập phương nên đường cao của hình nón bằng với cạnh của hình lập phương hay chiều cao \(h=1.\)

Với \(l\) là độ dài đường sinh của hình nón. Theo định lí Pytago, ta có :

 \(l^2=r^2+h^2 \Rightarrow l= \sqrt{1^2+ 0,5^2}=\dfrac{\sqrt{5}}{2}\).

Bài 16 trang 117 SGK Toán lớp 9 tập 2

Câu hỏi:

Cắt mặt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành 1 hình quạt. Biết bán kính của quạt  bằng độ dài đường sinh và độ dài cung bằng chu vi đáy.

Quan sát hình 94 và tính số đo cung của hình quạt.

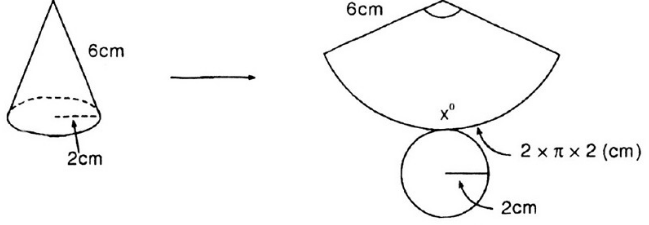
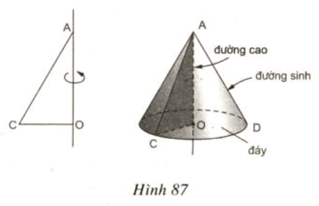
Phương pháp: 

+ Sử dụng công thức tính chu vi đường tròn bán kính \(r\) là \(C = 2\pi r.\)

+ Sử dụng công thức tính độ dài cung tròn bán kính \(R\) và số đo cung \(n^\circ \) là \(l = \dfrac{{\pi Rn}}{{180}}\) 

Lời giải:

+ Hình nón có bán kính đáy \(r = 2cm\)

+ Hình quạt có bán kính \(R = 6cm\)

Độ dài cung của hình quạt chính là chu vi đáy của hình nón và là: \(l = C =2\pi r = 2\pi .2 = 4\pi \left( {cm} \right)\)

Gọi \(x^\circ \,\left( {x > 0} \right)\) là số đo cung của hình quạt.

Khi đó độ dài cung là \(l = \dfrac{{\pi Rx}}{{180}} \Leftrightarrow \dfrac{{\pi .6.x}}{{180}} = 4\pi  \Leftrightarrow 6x = 720 \Leftrightarrow x = 120.\)  (thỏa mãn)

Vậy số đo cung của hình quạt tròn là \(120^\circ .\)

Bài 17 trang 117 SGK Toán lớp 9 tập 2

Câu hỏi:

Khi quay tam giác vuông để tạo ra một hình nón như hình 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là 30°, độ dài đường sinh là a. Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón

Lời giải:

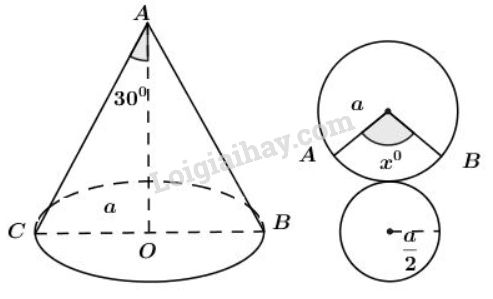
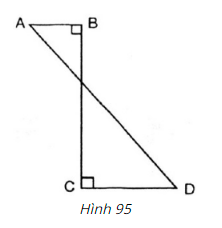
Vì \( \widehat {CAO}=30^0\) nên góc ở đỉnh của hình nón là \(\widehat {CAB}=2.30^0=60^0\)

Mà AB = AC

Nên \(∆ABC\) đều) (Tam giác cân có 1 góc bằng \(60^0\))

\(\Rightarrow BC = AB = AC=a\)

\(\Rightarrow\) Bán kính đáy của hình nón là:\( CO =\dfrac{BC}{2}=\dfrac{a}{2}\)

Chu vi đáy hình nón là \(C=2\pi.\dfrac{a}{2}=\pi .a\) 

Đường sinh của hình nón là \(a.\) Khai triển mặt xung quanh hình nón ta được hình quạt AOB có bán kính \(R = a.\)

Độ dài cung AB có số đo \(x^0,\) bán kính \(a\) là \(l=\dfrac{\pi ax}{180}\)

Vì độ dài cung \(AB\) bằng chu vi đáy hình nón nên ta có:

\(\dfrac{\pi. ax}{180}=\pi .a\) 

\(\Rightarrow\) \(x^0=180^0.\) 

Bài 18 trang 117 SGK Toán lớp 9 tập 2

Câu hỏi:

Hình \(ABCD\) (h95) khi quay quanh \(BC\) thì tạo ra: 

(A) Một hình trụ;

(B) Một hình nón;

(C) Một hình nón cụt;

(D) Hai hình nón;

(E) Hai hình trụ.

Hãy  chọn câu trả lời đúng.

Lời giải:

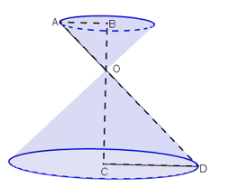
Gọi \(O\) là giao điểm của \(BC\) và \(AD.\)  

Khi quay  hình \(ABCD\) quanh \(BC\) có nghĩa là tam giác vuông \(OBA\) quanh \(OB\) và tam giác vuông \(OCD\) quanh \(OC.\)

Mỗi hình tam giác vuông trên quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ tạo ra \(2\) hình nón.

Vậy chọn D.

Sachbaitap.com