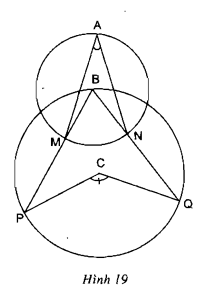
Bài 15, 16, 17, 18 trang 75 SGK Toán 9 tập 2 - Góc nội tiếpGiải bài 15, 16, 17, 18 trang 75 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Góc nội tiếp. Bài 17 Muốn xác định tâm của một đường tròn mà chỉ dùng êke thì phải làm như thế nào? Bài 15 trang 75 SGK Toán lớp 9 tập 2 Câu hỏi: Các khẳng định sau đúng hay sai? a) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau. b) Trong một đường tròn, các góc nội tiếp bằng nhau thì cùng chắn một cung. Lời giải: a) Đúng (Theo hệ quả: Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau) b) Sai, vì trong một đường tròn các góc nội tiếp bằng nhau có thể là chắn các cung bằng nhau hoặc cùng chắn một cung. Bài 16 trang 75 SGK Toán lớp 9 tập 2 Câu hỏi: Xem hình 19 ( hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C). a) Biết \(\widehat{MAN}\) = \(30^{\circ}\), tính \(\widehat{PCQ}\). b) Nếu \(\widehat{PCQ}\) =\(136^{\circ}\) thì \(\widehat{MAN}\) có số đo là bao nhiêu?
Lời giải: a) Xét đường tròn tâm \(B\) có: \(\widehat {MAN}\) là góc nội tiếp chắn cung \(MN\); \(\widehat {MBN}\) là góc ở tâm chắn cung \(MN\) nên \(\widehat {MAN} =\dfrac{1}{2}.\widehat {MBN}\) Lại xét đường tròn tâm \(C\) có \(\widehat {PBQ}\) là góc nội tiếp chắn cung \(PQ\); \(\widehat {PCQ}\) là góc ở tâm chắn cung \(PQ\) nên \(\widehat {PBQ} =\dfrac{1}{2}.\widehat {PCQ}\) \(\Rightarrow \widehat {MAN} = \dfrac{1}{4}.\widehat {PCQ}=\dfrac{1}{4}.30^0=120^0\) b) Theo a) ta có \(\widehat {MAN} = \dfrac{1}{4}.\widehat {PCQ}\) Nếu \(\widehat {PCQ} = 136^\circ\) thì\(\widehat {MAN} = \dfrac{1}{4}\widehat {PCQ}= \dfrac{{136^\circ }}{4} = 34^\circ .\) Bài 17 trang 75 SGK Toán lớp 9 tập 2 Câu hỏi: Muốn xác định tâm của một đường tròn mà chỉ dùng êke thì phải làm như thế nào? Lời giải:
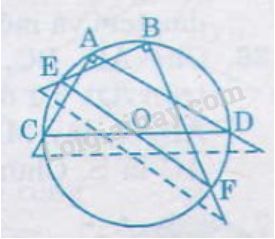
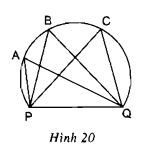
Vận dụng hệ quả: Góc nội tiếp chắn nửa đường tròn là góc vuông + Đặt đỉnh vuông của ê ke trùng với 1 điểm B bất kì trên đường tròn. Vẽ 2 dây cung BE, BF. Ta được tam giác BEF nội tiếp đường tròn đường kính EF + Đặt đỉnh vuông của ê ke trùng với 1 điểm A bất kì trên đường tròn. Vẽ 2 dây cung AC, AD. Ta được tam giác ACD nội tiếp đường tròn đường kính CD + Tâm đường tròn chính là giao điểm O của hai cạnh huyền DC và EF của hai tam giác vuông nội tiếp đường tròn. Bài 18 trang 75 SGK Toán lớp 9 tập 2 Câu hỏi: Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn \(PQ\). Bóng được đặt ở các vị trí \(A, B, C\) trên một cung tròn như hình 20. Hãy so sánh các góc \(\widehat{PAQ}\), \(\widehat{PBQ}\), \(\widehat{PCQ}\).
Lời giải: Với các vị trí \(A, B, C\) trên một cung tròn thì ta được các góc nội tiếp \(\widehat{PAQ}\),\(\widehat{PBQ}\), \(\widehat{PCQ}\) cùng chắn một cung \(\overparen{PQ}\), nên suy ra \(\widehat{PAQ}\) = \(\widehat{PBQ}\) = \(\widehat{PCQ}\). Vậy với các vị trí trên thì các góc sút đều bằng nhau, không có góc sút nào rộng hơn. Sachbaitap.com
Xem thêm tại đây:
Bài 3. Góc nội tiếp
|
-

Bài 19, 20, 21, 22, 23, 24, 25, 26 trang 75, 76 SGK Toán 9 tập 2 - Luyện tập
Giải bài 19 trang 75; bài 20, 21, 22, 23, 24, 25, 26 trang 76 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Luyện tập Góc nội tiếp. Bài 25 Dựng một tam giác vuông, biết cạnh huyền dài 4cm và một cạnh góc vuông dài 2,5cm.
-

Bài 27, 28, 29, 30 trang 79 SGK Toán 9 tập 2 - Góc tạo bởi tia tiếp tuyến và dây cung
Giải bài 27, 28, 29, 30 trang 79 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Góc tạo bởi tia tiếp tuyến và dây cung. Bài 27 Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn.
-

Bài 31, 32, 33, 34, 35 trang 79, 80 SGK Toán 9 tập 2 - Luyện tập
Giải bài 31 trang 79; bài 32, 33, 34, 35 trang 80 sách giáo khoa (SGK) Toán lớp 9 tập 2 bài Luyện tập. Bài 35 Trên bờ biển có một ngọn hải đăng cao 40m. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trông thấy ngọn đèn này.

 Tải ngay
Tải ngay