Tải ngay
Bài 1.5 trang 11 sách bài tập (SBT) – Hình học 12.Chứng minh rằng mỗi hình đa diện có ít nhất 4 đỉnh. Chứng minh rằng mỗi hình đa diện có ít nhất 4 đỉnh. Hướng dẫn làm bài: Gọi M1 là một mặt của hình đa diện (H). Gọi A, B, C là ba đỉnh liên tiếp của M1. Khi đó AB, BC là hai cạnh của (H). Gọi M2 là mặt khác với M1 và có chung cạnh AB với M1. Khi đó M2 còn có ít nhất một đỉnh D khác với A và B. Nếu \(D \equiv C\) thì M1 và M2 có hai cạnh chung AB và BC , điều này vô lý. Vậy D phải khác C. Do đó (H) có ít nhất bốn đỉnh A, B, C, D. Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 1. Khái niệm về khối đa diện - SBT Toán 12
|
-
Bài 1.6 trang 14 sách bài tập (SBT) – Hình học 12
Tính sin của góc tạo bởi hai mặt kề nhau (tức là hai mặt có một cạnh chung) của một tứ diện đều.
-
Bài 1.7 trang 14 sách bài tập (SBT) – Hình học 12.
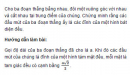
Cho ba đoạn thẳng bẳng nhau, đôi một vuông góc với nhau và cắt nhau tại trung điểm của chúng. Chứng minh rằng các đầu mút của ba đoạn thẳng ấy là các đỉnh của một hình bát diện đều.
-
Bài 1.8 trang 14 sách bài tập (SBT) – Hình học12
Cho một khối bát diện đều. Hãy chỉ ra một mặt phẳng đối xứng, một tâm đối xứng và một trục đối xứng của nó.
-
Bài 1.9 trang 14 sách bài tập (SBT) – Hình học 12
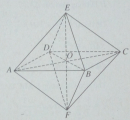
Cho khối bát diện đều ABCDEF (hình vẽ). Gọi O là giao điểm của AC và BD, M và N theo thứ tự là trung điểm của AB và AE. Tính diện tích thiết diện tạo bởi khối bát diện đó và mặt phẳng (OMN).
