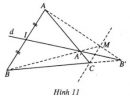
Bài 20 trang 8 SBT Hình học 10 Nâng caoGiải bài tập Bài 20 trang 8 SBT Hình học 10 Nâng cao Cho tam giác ABC và các điểm \(A_1, B_1, C_1\) lần lượt nằm trên các đường thẳng \(BC, CA, AB\). Gọi \(A_2, B_2, C_2\) lần lượt là các điểm đối xứng với \(A_1, B_1, C_1\) qua trung điểm của \(BC, CA, AB\). Chứng minh rằng a) Nếu ba điểm \(A_1, B_1, C_1\) thẳng hàng thì ba điểm \(A_2, B_2, C_2\) cũng thế; b) Nếu ba đường thẳng \(AA_1, BB_1, CC_1\) đồng quy hoặc song song thì ba đường thẳng \(AA_2, BB_2, CC_2\) cũng thế. Giải Ta gọi \(k, l, m\) là các số sao cho \(\overrightarrow {{A_1}B} = k\overrightarrow {{A_1}C};\) \(\overrightarrow {{B_1}C} = l\overrightarrow {{B_1}A};\) \(\overrightarrow {{C_1}A} = m\overrightarrow {{C_1}B} \). Chú ý rằng ba điểm \(A_1, B_1, C_1\) lần lượt là đối xứng với ba điểm \(A_2, B_2, C_2\) qua trung điểm đoạn thẳng \(BC, CA, AB\) nên ta có \(\overrightarrow {{A_2}C} = k\overrightarrow {{A_2}B};\) \(\overrightarrow {{B_2}A} = l\overrightarrow {{B_2}C};\) \(\overrightarrow {{C_2}B} = m\overrightarrow {{C_2}A} \) Từ đó bằng cách áp dụng định lí thuận và đảo của định lí Mê-nê-la-uýt ( hoặc Xê- va) ta chứng minh được câu a) ( hoặc câu b)). Sachbaitap.com
Xem thêm tại đây:
Bài 4. Tích của một vec tơ với một số.
|

 Tải ngay
Tải ngay