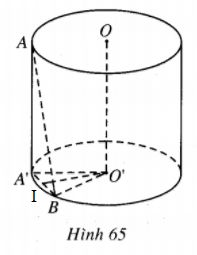
Bài 21 trang 58 Sách bài tập Hình học lớp 12 Nâng caoCho hình trụ có bán kính đáy bằng R, Cho hình trụ có bán kính đáy bằng R, chiều cao OO’ bằng h, A và B là hai điểm thay đổi trên hai đường tròn đáy sao cho AB = a không đổi \(\left( {h < a < \sqrt {{h^2} + 4{R^2}} } \right)\). 1) Chứng minh góc giữa hai đường thẳng AB và OO’ không đổi. 2) Chứng minh khoảng cách giữa hai đường thẳng AB và OO’ không đổi. Giải
1) Gọi AA’ là một đường sinh của hình trụ thì AA’=h và \({\rm{AA'//}}OO'\), khi ấy \(\alpha = \widehat {BAA'}\) là góc giữa AB và OO’ và \(\cos \alpha = {{AA'} \over {AB}} = {h \over a}.\) Điều này khẳng định góc giữa AB và OO’ không đổi. 2) Gọi I là trung điểm của A’B thì có \(O'I \bot mp(AA'B),\) mặt khác \(OO'//mp(AA'B),\) vậy O’I là khoảng cách giữa AB và OO’. Vì O’I là trung tuyến của tam giác A’O’B có ba cạnh là \(A'B = \sqrt {{a^2} - {h^2}} ,O'A' = O'B' = R\) nên O'I có độ dài không đổi. Dễ thấy \(O'I = \sqrt {{R^2} - {{{a^2} - {h^2}} \over 4}} .\) Sachbaitap.com
Xem lời giải SGK - Toán 12 Nâng cao - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 2, 3 : Khái niệm về mặt tròn xoay. Mặt trụ, hình trụ và khối trụ
|
-
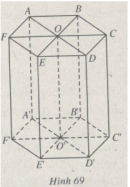
Bài 25 trang 59 Sách bài tập Hình học lớp 12 Nâng cao
Cho hình lăng trụ lục giác đều ABCDEF.A’B’C’D’E’F’ có

 Tải ngay
Tải ngay