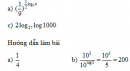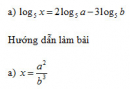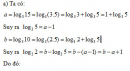Bài 2.11 trang 103 Sách bài tập (SBT) Giải tích 12

Hãy viết các số sau theo thứ tự tăng dần:

a) \({(0,3)^\pi },{(0,3)^{0,5}},{(0,3)^{\frac{2}{3}}},{(0,3)^{3,1415}}\)                                    

b) \(\sqrt {{2^\pi }} ,{(1,9)^\pi },{(\frac{1}{{\sqrt 2 }})^\pi },{\pi ^\pi }\)

c) \({5^{ - 2}},{5^{ - 0,7}},{5^{\frac{1}{3}}},{(\frac{1}{5})^{2,1}}\)                                                      

d) \({(0,5)^{ - \frac{2}{3}}},{(1,3)^{ - \frac{2}{3}}},{\pi ^{ - \frac{2}{3}}},{(\sqrt 2 )^{ - \frac{2}{3}}}\)

Hướng dẫn làm bài:

a) \({(0,3)^\pi };{(0,3)^{3,1415}};{(0,3)^{\frac{2}{3}}};{(0,3)^{0,5}}\)

(vì cơ số a = 0,3 < 1 và \(\pi  > 3,1415 > \frac{2}{3} > 0,5\) )

b)  \({(\frac{1}{{\sqrt 2 }})^\pi };{(\sqrt 2 )^\pi };{(1,9)^\pi };{\pi ^\pi }\)  (vì  \(\frac{1}{{\sqrt 2 }} < \sqrt 2  < 1,9 < \pi \) )

c) \({(\frac{1}{5})^{2,1}};{5^{ - 2}};{5^{ - 0,7}};{5^{\frac{1}{3}}}\)

d) \({\pi ^{ - \frac{2}{3}}};{(\sqrt 2 )^{ - \frac{2}{3}}};{(1,3)^{ - \frac{2}{3}}};{(0,5)^{ - \frac{2}{3}}}\).

Sachbaitap.com