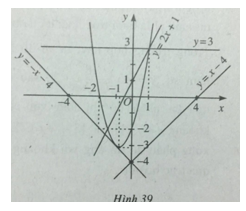
Bài 22 trang 42 Sách bài tập (SBT) Toán 10

Tìm giao điểm của parabol \(y = 2{x^2} + 3x - 2\) với các đường thẳng

a) y = 2x + 1 ; 

b) y = x – 4 ; 

c) y = -x – 4 ; 

d) y = 3.

Hướng dẫn. Để xác định hoành độ giao điểm của hai đồ thị có phương trình tương ứng là và ta phải giải phương trình \(f(x) = g(x)\)

Gợi ý làm bài

a) Xét phương trình: 

\(2{x^2} + 3x - 2 = 2x + 1 \Leftrightarrow 2{x^2} + x - 3 = 0 \Leftrightarrow \left[ \matrix{
{x_1} = 1 \hfill \cr
{x_2} = - {3 \over 2} \hfill \cr} \right.\)

Vậy parabol đã cho và đường thẳng y = 2x + 1 có hai giao điểm là (1;3) và \(( - {3 \over 2}; - 2)\)

b) Xét phương trình \(2{x^2} + 3x - 2 = x - 4\)

\(\eqalign{
& \Leftrightarrow 2{x^2} + 2x + 2 = 0 \cr
& \Leftrightarrow 2{x^2} + 2x + 2 = 0 \cr
& \Leftrightarrow {x^2} + x + 1 = 0(*) \cr} \)

Phương trình (*) có biệt thức \(\Delta  = 1 - 4 =  - 3 < 0\) , do đó phương trình vô nghiệm.

Vậy parabol đã cho và đường thẳng y = x – 4 không có giao điểm.

c) Xét phương trình

\(2{x^2} + 3x - 2 =  - x - 4 \Leftrightarrow 2{x^2} + 4x + 2 = 0\)

\({x^2} + 2x + 1 = 0 =  > x =  - 1\)

Vậy parabol đã cho và đường thẳng y = -x – 4 tiếp xúc nhau tại điểm có tọa độ (-1;-3).

Đồ thị được vẽ trên hình 39

d) Xét phương trình 

\(2{x^2} + 3x - 2 = 3 \Leftrightarrow 2{x^2} + 3x - 5 = 0 \Leftrightarrow \left[ \matrix{
{x_1} = 1 \hfill \cr
{x_2} = - {5 \over 2} \hfill \cr} \right.\)

Vậy có hai giao điểm là (1;3) và \(( - {5 \over 2};3)\)

Sachbaitap.net