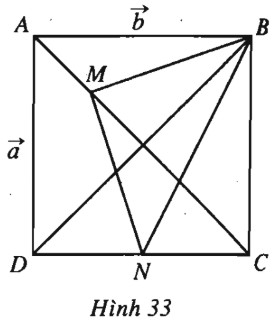
Bài 23 trang 41 SBT Hình học 10 Nâng caoGiải bài tập Bài 23 trang 41 SBT Hình học 10 Nâng cao Cho hình vuông \(ABCD\), điểm \(M\) nằm trên đoạn thẳng \(AC\) sao cho \(AM = \dfrac{{AC}}{4}\). Gọi \(N\) là trung điểm của đoạn thẳng \(DC\). Chứng minh rằng \(BMN\) là tam giác vuông cân. Giải
Đặt \(\overrightarrow {AD} = \overrightarrow a , \overrightarrow {AB} = \overrightarrow b .\) Khi đó, ta có \(\overrightarrow {AM} = \dfrac{1}{4}\overrightarrow {AC} = \dfrac{1}{4}(\overrightarrow a + \overrightarrow b ),\) \( \overrightarrow {AN} = \overrightarrow {AD} + \overrightarrow {DN} = \overrightarrow a + \dfrac{{\overrightarrow b }}{2}.\) Từ đó suy ra \(\begin{array}{l}\overrightarrow {MB} = \overrightarrow {AB} - \overrightarrow {AM}\\ = \overrightarrow b - \dfrac{1}{4}(\overrightarrow a + \overrightarrow b )\\ = \dfrac{1}{4}( - \overrightarrow a + 3\overrightarrow b ).\\\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM}\\ = \overrightarrow a + \dfrac{{\overrightarrow b }}{2} - \dfrac{1}{4}(\overrightarrow a + \overrightarrow b ) \\= \dfrac{1}{4}(3\overrightarrow a + \overrightarrow b ).\end{array}\) Ta có \(\begin{array}{l}\overrightarrow {MB} .\overrightarrow {MN}\\ = \dfrac{1}{{16}}( - \overrightarrow a + 3\overrightarrow b )(3\overrightarrow a + \overrightarrow b )\\= \dfrac{1}{{16}}\left( { - 3\overrightarrow a + 3\overrightarrow b + 8\overrightarrow a .\overrightarrow b } \right) = 0.\\{\overrightarrow {MB} ^2} = \dfrac{1}{{16}}( - \overrightarrow a + 3\overrightarrow b ) \\= \dfrac{1}{{16}}({\overrightarrow a ^2} + 9{\overrightarrow b ^2} - 6\overrightarrow a .\overrightarrow b ) = \dfrac{5}{8}{\overrightarrow a ^2}.\\{\overrightarrow {MN} ^2} = \dfrac{1}{{16}}{\left( {3\overrightarrow a + \overrightarrow b } \right)^2}\\ = \dfrac{1}{{16}}\left( {9{{\overrightarrow a }^2} + {{\overrightarrow b }^2} + 6\overrightarrow a .\overrightarrow b } \right)\\ = \dfrac{5}{8}{\overrightarrow a ^2}.\end{array}\) Vậy \(MB \bot MN\) và \(MB=MN\), tam giác \(BMN\) vuông cân tại đỉnh \(M.\) Sachbaitap.com
Xem thêm tại đây:
Bài 2. Tích vô hướng của hai vec tơ
|

 Tải ngay
Tải ngay