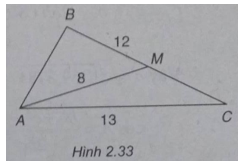
Bài 2.51 trang 104 Sách bài tập (SBT) Toán Hình học 10

Bình chọn:

4 trên 2 phiếu

Tam giác ABC có BC

Tam giác ABC có BC = 12, CA = 13, trung tuyến AM = 8

a) Tính diện tích tam giác ABC;

b) Tính góc B.

Gợi ý làm bài

(h.2.33)

Theo công thức Hê – rông ta có:

\({S_{AMC}} = \sqrt {{{27} \over 2}\left( {{{27} \over 2} - 13} \right)\left( {{{27} \over 2} - 6} \right)\left( {{{27} \over 2} - 8} \right)} \)

\( = {{9\sqrt {55} } \over 4}\)

\({S_{ABC}} = 2{S_{AMC}} = {{9\sqrt {55} } \over 2}\)

Mặt khác ta có \(A{M^2} = {{{b^2} + {c^2}} \over 2} - {{{a^2}} \over 4}\) hay \(2A{M^2} = {b^2} + {c^2} - {{{a^2}} \over 2}\)

Do đó

\(\eqalign{
& A{B^2} = {c^2} = 2A{M^2} - {b^2} + {{{a^2}} \over 2} \cr
& = 2.64 - 169 + 72 = 31 \cr} \)

\( = > c = \sqrt {31} \)

\(\eqalign{
& \cos B = {{{a^2} + {c^2} - {b^2}} \over {2ac}} = {{144 + 31 - 169} \over {24\sqrt {31} }} \cr
& \approx 0,045 = > \widehat B \approx {87^0}25' \cr} \)

Sachbaitap.net

Báo lỗi - Góp ý

Xem lời giải SGK - Toán 10 - Xem ngay

>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.