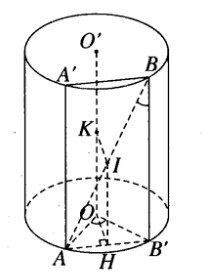
Bài 2.9 trang 50 sách bài tập (SBT) – Hình học 12.Một khối trụ có bán kính đáy bằng r và chiều cao bằng . Một khối trụ có bán kính đáy bằng r và chiều cao bằng \(r\sqrt 3 \). Gọi A và B là hai điểm trên hai đường tròn đáy sao cho góc được tạo thành giữa đường thẳng AB và trục của khối trụ bằng 300. a) Tính diện tích của thiết diện qua AB và song song với trục của khối trụ. b) Tính góc giữa hai bán kính đáy qua A và B. c) Xác định và tính độ dài đoạn vuông góc chung của AB và trục của khối trụ. Hướng dẫn làm bài:
a) Từ A và B dựng các đường sinh AA’ và BB’ ta có thiết diện qua AB và song song với trục là hình chữ nhật AA’BB’. Góc giữa AB và trục chính là góc \(\widehat {ABB'}\) . Do đó, \(\widehat {ABB'} = {30^0}\). Vậy \(AB' = BB'\tan {30^0} = r\sqrt 3 .{1 \over {\sqrt 3 }} = r\) Do đó diện tích tứ giác AA’BB’ là \({S_{{\rm{AA}}'BB'}} = AB'.BB' = r.r\sqrt 3 = {r^2}\sqrt 3 \) b) Góc giữa hai bán kính đáy OA và O’B là \(\widehat {AOB'}\) và \(\widehat {A'O'B}\) Vì AB’ = r nên AOB’ là tam giác đều , do đó \(\widehat {AOB}' = {60^0}\) c) Mặt phẳng (ABB’) chứa AB và song song với trục OO’ của hình trụ. Gọi H là trung điểm của AB’. Ta có \(OH \bot (ABB')\) . Đường thẳng qua H song song với OO’ cắt AB tại I. Dựng IK // HO cắt OO’ tại K. Ta chứng minh được IK là đoạn vuông góc chung của AB và OO’. Ta có \(IK = HO = {{r\sqrt 3 } \over 2}\) Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 1. Khái niệm về mặt tròn xoay
|
-
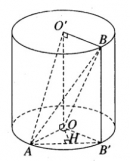
Bài 2.10 trang 51 sách bài tập (SBT) – Hình học 12
Một hình trụ có các đáy là hai hình tròn tâm O và O’ bán kính r và có đường cao . Gọi A là một điểm trên đường tròn tâm O và B là một điểm trên đường tròn tâm O’ sao cho OA vuông góc với O’B.
-
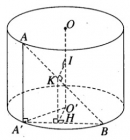
Bài 2.11 trang 51 sách bài tập (SBT) – Hình học 12
Một hình trụ có bán kính đáy bằng 50 cm và có chiều cao h = 50 cm.
-
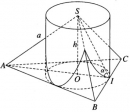
Bài 2.12 trang 51 sách bài tập (SBT) – Hình học 12
Tính diện tích xung quanh của hình trụ có đường tròn đáy là đường tròn nội tiếp tam giác đáy của hình chóp và có chiều cao bằng chiều cao của hình chóp. Các mặt bên SAB , SBC , SCA cắt hình trụ theo những giao tuyến như thế nào?
-
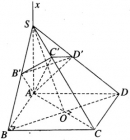
Bài 2.13 trang 63 sách bài tập (SBT) – Hình học 12
Trong mặt phẳng cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ta lấy một điểm S tùy ý, dựng mặt phẳng đi qua A và vuông góc với đường thẳng SC. Mặt phẳng cắt SB, SC, SD lần lượt tại B’ , C’, D’.

 Tải ngay
Tải ngay