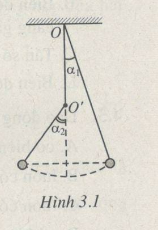
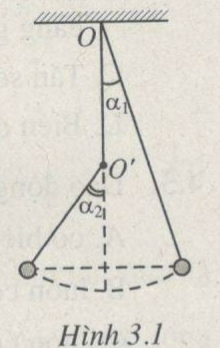
Bài 3.15 trang 11 Sách bài tập (SBT) Vật Lí 12Một con lắc đơn dài 1,0 m. Phía dưới điểm treo O trên phương thẳng đứng có một chiếc đinh đóng chắc vào điểm O' cách O một đoạn OO' = 0,5 m, sao cho con lắc vấp vào đinh khi dao động (H.3.1). 3.15. Một con lắc đơn dài 1,0 m. Phía dưới điểm treo O trên phương thẳng đứng có một chiếc đinh đóng chắc vào điểm O' cách O một đoạn OO' = 0,5 m, sao cho con lắc vấp vào đinh khi dao động (H.3.1). Kéo con lắc lệch khỏi phương thẳng đứng một góc \(\alpha\)1 =10° rồi thả không vận tốc đầu. Bỏ qua ma sát. Hãy tính : a) Biên độ góc của con lắc ở hai bên vị trí cân bằng. b) Chu kì dao động của con lắc. Lấy g = 9,8 m/s2. Hình 3.1 Hướng dẫn giải chi tiết a) Biên độ góc của con lắc ở hai bên vị trí cân bằng. Theo định luật bảo toàn năng lượng ta suy ra hai vị trí biên phải ở cùng 1 độ cao (H3.1.G)
\(\eqalign{ b) Chu kì dao động của con lắc \(\eqalign{ Sachbaitap.com
Xem lời giải SGK - Vật lí 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài 3. Con lắc đơn
|
-
Bài 4.1 trang 11 Sách bài tập (SBT) Vật Lí 12
Một con lắc dao động tắt dần chậm. Cứ sau mỗi chu kì, biên độ giảm 3%. Phần năng lượng của con lắc bị mất đi trong một dao động toàn phân là bao nhiêu ?
-
Bài 4.2, 4.3, 4.4, 4.5, 4.6 trang 12 Sách bài tập (SBT) Vật Lí 12
Một con lắc lò xo đang dao động tắt dần. Người ta đo được độ giảm tương đối của biên độ trong ba chu kì đầu tiên là 10%. Độ giảm tương đối của thế năng tương ứng là bao nhiêu ?
-
Bài 4.7, 4.8 trang 13 Sách bài tập (SBT) Vật Lí 12
Một vật dao động tắt dần có các đại lượng nào sau đây giảm liên tục theo thời gian ?

 Tải ngay
Tải ngay