Bài 32, 33, 34, 35, 36, 37 trang 19, 20 SGK Toán 9 tập 1 - Luyện tậpGiải bài 32, 33, 34 trang 19; bài 35, 36, 37 trang 20 sách giáo khoa Toán lớp 9 tập 1 bài Luyện tập. Bài 36 Mỗi khẳng định sau đúng hay sai ? Vì sao ? Bài 37 Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1cm, cho bốn điểm (M, N, P, Q) (h.3). Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNPQ. Bài 32 trang 19 SGK Toán lớp 9 tập 1 Câu hỏi: Tính: a) \( \sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01}\) b) \( \sqrt{1,44.1,21-1,44.0,4}\) c) \( \sqrt{\dfrac{165^{2}-124^{2}}{164}}\) d) \( \sqrt{\dfrac{149^{2}-76^{2}}{457^{2}-384^{2}}}\) Lời giải: a) Ta có: \(\sqrt{1\dfrac{9}{16}.5\dfrac{4}{9}.0,01}=\sqrt{\dfrac{1.16+9}{16}.\dfrac{5.9+4}{9}.\dfrac{1}{100}}\) \(=\sqrt{\dfrac{16+9}{16}.\dfrac{45+4}{9}.\dfrac{1}{100}}\) \(=\sqrt{\dfrac{25}{16}.\dfrac{49}{9}.\dfrac{1}{100}}\) \(=\sqrt{\dfrac{25}{16}}.\sqrt{\dfrac{49}{9}}.\sqrt{\dfrac{1}{100}}\) \(=\dfrac{\sqrt{25}}{\sqrt{16}}.\dfrac{\sqrt{49}}{\sqrt{9}}.\dfrac{\sqrt{1}}{\sqrt{100}}\) \(=\dfrac{\sqrt{5^2}}{\sqrt{4^2}}.\dfrac{\sqrt{7^2}}{\sqrt{3^2}}.\dfrac{1}{\sqrt{10^2}}\) \(=\dfrac{5}{4}.\dfrac{7}{3}.\dfrac{1}{10}=\dfrac{5.7.1}{4.3.10}=\dfrac{35}{120}=\dfrac{7}{24}.\) b) Ta có: \(\sqrt{1,44.1,21-1,44.0,4} \)\(= \sqrt{1,44(1,21-0,4)}\) \(=\sqrt{1,44.0,81}\) \(=\sqrt{1,44}.\sqrt{0,81}\) \(=\sqrt{1,2^2}.\sqrt{0,9^2}\) \(=1,2.0,9=1,08\). c) Ta có: \(\sqrt{\dfrac{165^{2}-124^{2}}{164}}\)\(=\sqrt{\dfrac{(165-124)(165+124)}{164}}\) \(=\sqrt{\dfrac{41.289}{41.4}}\) \(=\sqrt{\dfrac{289}{4}}\) \(=\dfrac{\sqrt{289}}{\sqrt{4}}\) \(=\dfrac{\sqrt{17^2}}{\sqrt{2^2}}\) \(=\dfrac{17}{2}\). d) Ta có: \(\sqrt{\dfrac{149^{2}-76^{2}}{457^{2}-384^{2}}}\) \(=\sqrt{\dfrac{(149-76)(149+76)}{(457-384)(457+384)}}\) \(=\sqrt{\dfrac{73.225}{73.841}}\) \(=\sqrt{\dfrac{225}{841}}\) \(=\sqrt {\dfrac{15^2}{29^2}} = \sqrt {{{\left( {\dfrac{{15}}{{29}}} \right)}^2}}=\dfrac{15}{29}\). Bài 33 trang 19 SGK Toán lớp 9 tập 1 Câu hỏi: Giải phương trình a) \(\sqrt 2 .x - \sqrt {50} = 0\) b) \(\sqrt 3 .x + \sqrt 3 = \sqrt {12} + \sqrt {27}\) c) \(\sqrt 3 .{x^2} - \sqrt {12} = 0\) d) \(\dfrac{x^2}{\sqrt 5 } - \sqrt {20} = 0\) Phương pháp: Sử dụng các công thức + \(\sqrt {AB} = \sqrt A .\sqrt B \,\left( {A;B \ge 0} \right)\) + \(\dfrac{\sqrt A}{\sqrt B}=\sqrt{\dfrac{A}{B}}\) (với \( A\ge 0;B>0\)) + \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l} Lời giải:
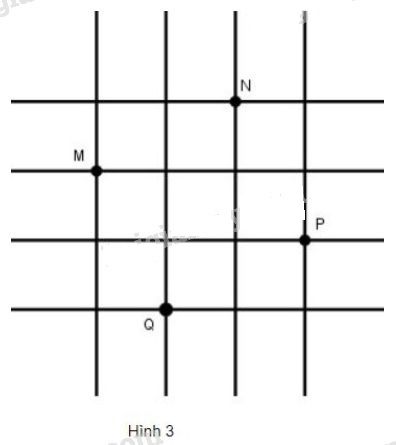
a) \(\sqrt{2}.x - \sqrt{50} = 0\) \(\Leftrightarrow \sqrt{2}x=\sqrt{50}\) \(\Leftrightarrow x=\dfrac{\sqrt{50}}{\sqrt{2}}\) \(\Leftrightarrow x =\sqrt{\dfrac{50}{2}}\) \(\Leftrightarrow x= \sqrt{25}\) \(\Leftrightarrow x= \sqrt{5^2}\) \(\Leftrightarrow x=5\). Vậy \(x=5\). b) \(\sqrt{3}.x + \sqrt{3} = \sqrt{12} + \sqrt{27}\) \( \Leftrightarrow \sqrt{3}.x = \sqrt{12} + \sqrt{27} - \sqrt{3}\) \(\Leftrightarrow \sqrt{3}.x=\sqrt{4.3}+\sqrt{9.3}- \sqrt{3}\) \(\Leftrightarrow \sqrt{3}.x=\sqrt{4}. \sqrt{3}+\sqrt{9}. \sqrt{3}- \sqrt{3}\) \(\Leftrightarrow \sqrt{3}.x=\sqrt{2^2}. \sqrt{3}+\sqrt{3^2}. \sqrt{3}- \sqrt{3}\) \(\Leftrightarrow \sqrt{3}.x=2 \sqrt{3}+3\sqrt{3}- \sqrt{3}\) \(\Leftrightarrow \sqrt{3}.x=(2+3-1).\sqrt{3}\) \(\Leftrightarrow \sqrt{3}.x=4\sqrt{3}\) \(\Leftrightarrow x=4\). Vậy \(x=4\). c) \(\sqrt{3}x^2-\sqrt{12}=0\) \(\Leftrightarrow \sqrt{3}x^2=\sqrt{12}\) \(\Leftrightarrow \sqrt{3}x^2=\sqrt{4.3}\) \(\Leftrightarrow \sqrt{3}x^2=\sqrt{4}.\sqrt 3\) \(\Leftrightarrow x^2=\sqrt{4}\) \(\Leftrightarrow x^2=\sqrt{2^2}\) \(\Leftrightarrow x^2=2\) \(\Leftrightarrow \sqrt{x^2}=\sqrt{2}\) \(\Leftrightarrow |x|= \sqrt 2\) \(\Leftrightarrow x= \pm \sqrt 2\). Vậy \(x= \pm\sqrt 2\). d) \(\dfrac{x^{2}}{\sqrt{5}}- \sqrt{20} = 0\) \(\Leftrightarrow \dfrac{x^2}{\sqrt{5}}=\sqrt{20}\) \(\Leftrightarrow x^2=\sqrt{20}.\sqrt{5}\) \(\Leftrightarrow x^2=\sqrt{20.5}\) \(\Leftrightarrow x^2=\sqrt{100}\) \(\Leftrightarrow x^2=\sqrt{10^2}\) \(\Leftrightarrow x^2=10\) \(\Leftrightarrow \sqrt{x^2}=\sqrt {10}\) \(\Leftrightarrow |x|=\sqrt{10}\) \(\Leftrightarrow x=\pm \sqrt{10}\). Vậy \(x= \pm \sqrt{10}\). Bài 34 trang 19 SGK Toán lớp 9 tập 1 Câu hỏi: Rút gọn các biểu thức sau: a) \( ab^{2}.\sqrt{\dfrac{3}{a^{2}b^{4}}}\) với \(a < 0,\ b ≠ 0\) b) \( \sqrt{\dfrac{27(a - 3)^{2}}{48}}\) với \(a > 3\) c) \( \sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}\) với \(a ≥ -1,5\) và \(b < 0.\) d) \((a - b).\sqrt{\dfrac{ab}{(a - b)^{2}}}\) với \(a < b < 0\) Phương pháp: Sử dụng các công thức: + \(\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt a}{\sqrt b}\) với \(a \ge 0; b>0\) + \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l} Lời giải: a) Ta có: \(ab^{2}.\sqrt{\dfrac{3}{a^{2}b^{4}}}=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2b^4}}\) \(=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2}.\sqrt{b^4}}\) \(=ab^2.\dfrac{\sqrt{3}}{\sqrt{a^2}.\sqrt{(b^2)^2}}\) \(=ab^2.\dfrac{\sqrt{3}}{|a|.|b^2|}\) \(=ab^2.\dfrac{\sqrt{3}}{-ab^2}=-\sqrt{3}\). (Vì \(a < 0 \) nên \(|a|=-a\) và \(b \ne 0\) nên \(b^2 >0 \Rightarrow |b^2|=b^2) \). b) Ta có: \(\sqrt{\dfrac{27(a - 3)^{2}}{48}}=\sqrt{\dfrac{27}{48}.(a-3)^2}\) \(=\sqrt{\dfrac{27}{48}}.\sqrt{(a-3)^2}\) \(=\sqrt{\dfrac{9.3}{16.3}}.\sqrt{(a-3)^2}\) \(=\sqrt{\dfrac{9}{16}}.\sqrt{(a-3)^2}\) \(=\sqrt{\dfrac{3^2}{4^2}}.\sqrt{(a-3)^2}\) \(=\dfrac{\sqrt {3^2}}{\sqrt {4^2}}.\sqrt{(a-3)^2}\) \(=\dfrac{3}{4}|a-3|=\dfrac{3}{4}(a-3)\). ( Vì \(a > 3\) nên \(a-3>0 \Rightarrow |a-3|=a-3) \) c) Ta có: \(\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}=\sqrt{\dfrac{3^2+2.3.2a+2^2.a^2}{b^2}}\) \(=\sqrt{\dfrac{3^2+2.3.2a+(2a)^2}{b^2}}=\sqrt{\dfrac{(3+2a)^2}{b^2}}\) \(=\dfrac{\sqrt{(3+2a)^2}}{\sqrt{b^2}}=\dfrac{|3+2a|}{|b|}\) Vì \(a \geq -1,5 \Rightarrow a+1,5>0\) \(\Leftrightarrow 2(a+1,5)>0\) \( \Leftrightarrow 2a+3>0\) \( \Leftrightarrow 3+2a>0\) \(\Rightarrow |3+2a|=3+2a\) Vì \(b<0\Rightarrow |b|=-b\) Do đó: \(\dfrac{|3+2a|}{|b|}=\dfrac{3+2a}{-b} =-\dfrac{3+2a}{b}\). Vậy \(\sqrt{\dfrac{9+12a+4a^{2}}{b^{2}}}=-\dfrac{3+2a}{b}\). d) Ta có: \((a - b).\sqrt{\dfrac{ab}{(a - b)^{2}}}=(a-b).\dfrac{\sqrt{ab}}{\sqrt{(a-b)^2}}\) \(=(a-b).\dfrac{\sqrt{ab}}{|a-b|}\) \(=(a-b).\dfrac{\sqrt{ab}}{-(a-b)}=-\sqrt{ab}\). (Vì \(a < b < 0\) nên \(a-b<0\Rightarrow |a-b|=-(a-b)\) và \(ab>0).\) Bài 35 trang 20 SGK Toán lớp 9 tập 1 Câu hỏi: Tìm x biết: a) \(\sqrt {{{\left( {x - 3} \right)}^2}} = 9\) b) \(\sqrt {4{{\rm{x}}^2} + 4{\rm{x}} + 1} = 6\) Lời giải: a) Ta có: \(\sqrt {{{\left( {x - 3} \right)}^2}} = 9 \Leftrightarrow \left| {x - 3} \right| = 9\) \( \Leftrightarrow \left[ \matrix{ \( \Leftrightarrow \left[ \matrix{ Vậy phương trình đã cho có hai nghiệm: \(x = 12\) và \(x = -6\). b) Ta có: \(\sqrt{4x^2+4x+1}=6 \Leftrightarrow \sqrt{2^2x^2+4x+1}=6\) \(\Leftrightarrow \sqrt{(2x)^2+2.2x+1^2}=6\) \(\Leftrightarrow \sqrt{(2x+1)^2}=6\) \(\Leftrightarrow |2x+1| =6\) \(\eqalign{ Vậy phương trình có \(2\) nghiệm \(x = \dfrac{5}{2}\) và \(x=\dfrac{-7}{2}\). Bài 36 trang 20 SGK Toán lớp 9 tập 1 Câu hỏi: Mỗi khẳng định sau đúng hay sai ? Vì sao ? a) \(0,01 = \sqrt {0,0001} \); b) \(- 0,5 = \sqrt { - 0,25} \); c) \(\sqrt {39} < 7\) và \(\sqrt {39} > 6\); d) \(\left( {4 - 13} \right).2{\rm{x}} < \sqrt 3 \left( {4 - \sqrt {13} } \right) \Leftrightarrow 2{\rm{x}} < \sqrt {3} \). Phương pháp: + \( \sqrt{A}\) xác định (hay có nghĩa) khi \(A \ge 0\). +) Sử dụng định lí so sánh hai căn bậc hai: \(a < b \Leftrightarrow \sqrt{a} < \sqrt{b}\), với \(a,\ b \ge 0\). + \(a.c >b.c \Leftrightarrow a> b\) , với \( c>0\). Lời giải: a) Đúng. Vì \(\sqrt {0,0001} = \sqrt {0,{{01}^2}} = 0,01\) Vì \(VP=\sqrt{0,0001}=\sqrt{0,01^2}=0,01=VT\). b) Sai. Vì vế phải không có nghĩa do số âm không có căn bậc hai. c) Đúng. Vì: \(36 < 39 < 49\) \(\Leftrightarrow \sqrt {36} < \sqrt {39} < \sqrt {49} \) \(\Leftrightarrow \sqrt {{6^2}} < \sqrt {39} < \sqrt {{7^2}} \) \(\Leftrightarrow 6 < \sqrt {39} < 7\) Hay \(\sqrt{39}>6\) và \( \sqrt{39} < 7\). d) Đúng. Xét bất phương trình đề cho: \((4-\sqrt{13}).2x<\sqrt 3 .(4-\sqrt{13})\) \((1)\) Ta có: \(16>13 \Leftrightarrow \sqrt{16} > \sqrt{13}\) \(\Leftrightarrow \sqrt{4^2}> \sqrt{13}\) \(\Leftrightarrow 4> \sqrt{13}\) \(\Leftrightarrow 4-\sqrt{13}>0\) Chia cả hai vế của bất đẳng thức \((1)\) cho số dương \((4-\sqrt{13})\), ta được: \(\dfrac{(4-\sqrt{13}).2x}{(4-\sqrt{13})} <\dfrac{\sqrt 3 .(4-\sqrt{13})}{(4-\sqrt{13})}\) \(\Leftrightarrow 2x < \sqrt 3.\) Vậy phép biến đổi tương đương trong câu d là đúng. Bài 37 trang 20 SGK Toán lớp 9 tập 1 Câu hỏi: Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1cm, cho bốn điểm (M, N, P, Q) (h.3). Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNPQ.
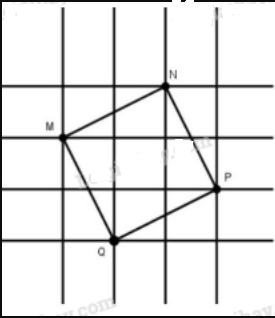
Phương pháp: + Sử dụng định lí Py-ta-go trong tam giác vuông. + Công thức tính diện tích hình vuông cạnh \(a\) là: \(S=a^2\). + Dấu hiệu nhận biết hình vuông: hình thoi có hai đường chéo bằng nhau (hay tứ giác có bốn cạnh bằng nhau và có hai đường chéo bằng nhau) thì là hình vuông. Lời giải: Nối các điểm ta có tứ giác \(MNPQ\)
Tứ giác \(MNPQ\) có: - Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài \(2cm\), chiều rộng \(1cm\). Do đó theo định lí Py-ta-go, ta có: \(MN=NP=PQ=QM=\sqrt{2^{2}+1^{2}}=\sqrt{5} (cm)\). Hay \(MNPQ\) là hình thoi. - Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài \(3cm\), chiều rộng \(1cm\) nên theo định lý Py-ta-go ta có độ dài đường chéo là: \(MP=NQ=\sqrt{3^{2}+1^{2}}=\sqrt{10}(cm).\) Như vậy hình thoi \(MNPQ\) có hai đường chéo bằng nhau nên \(MNPQ\) là hình vuông. Vậy diện tích hình vuông \(MNPQ\) bằng \(MN^{2}=(\sqrt{5})^{2}=5(cm^2)\). Sachbaitap.com
Xem thêm tại đây:
Bài 4. Liên hệ giữa phép chia và phép khai phương
|
-
Bài 38, 39, 40, 41, 42 trang 23 SGK Toán 9 tập 1 - Bảng căn bậc hai
Giải bài 38, 39, 40, 41, 42 trang 23 sách giáo khoa Toán lớp 9 tập 1 bài Bảng căn bậc hai. Dùng bảng số để tìm căn bậc hai số học của mỗi số sau đây rồi dùng máy tính bỏ túi kiểm tra và so sánh kết quả.

 Tải ngay
Tải ngay