Tải ngay
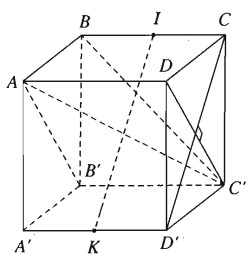
Bài 3.46 trang 164 Sách bài tập (SBT) Hình học 11Cho hình lập phương ABCD.A’B’C’D’. Hãy tính góc của các cặp đường thẳng sau đây: a) AB’ và BC’ b) AC’ và CD’ Cho hình lập phương ABCD.A’B’C’D’. Hãy tính góc của các cặp đường thẳng sau đây: a) AB’ và BC’ b) AC’ và CD’ Giải:
a) Ta có \(AB'\parallel DC'\). Gọi là góc giữa AB’và BC’, khi đó \(\alpha = \widehat {DC'B}\). Vì tam giác BC’D đều nên \(\alpha = {60^0}\) b) Gọi \(\beta \) là góc giữa AC’ và CD’. Vì CD’⊥C’D và CD’⊥AD ( do AD⊥(CDD’C’) Ta suy ra CD’⊥(ADC’B’) Vậy CD’⊥AC’ hay \(\beta = {90^0}\) Chú ý. Ta có thể chứng minh \(\beta = {90^0}\) bằng cách khác như sau: Gọi I và K lần lượt là trung điểm của các cạnh BC và A’D’. Ta có \(IK\parallel C{\rm{D}}'\). Dễ dàng chứng minh được AIC’K là một hình bình hành có bốn cạnh bằng nhau và đó là một hình thoi. Vậy AC’⊥IK hay AC’⊥CD’ và góc \(\beta = {90^0}\). Sachbaitap.com Xem lời giải SGK - Toán 11 - Xem ngay >> Học trực tuyến Lớp 11 cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng. Cam kết giúp học sinh lớp 11 học tốt, hoàn trả học phí nếu học không hiệu quả.
|
