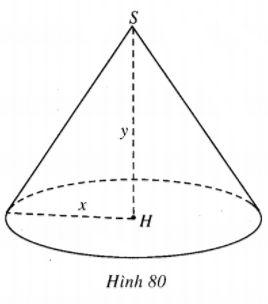
Bài 36 trang 61 Sách bài tập Hình học lớp 12 Nâng cao

Tìm hình nón có thể tích lớn nhất khi diện tích toàn phần của nó bằng diện tích hình tròn bán kính a cho trước.

Giải

Kí hiệu bán kính đáy và chiều cao hình nón lần lượt là x và y (x, y > 0). Khi đó, diện tích toàn phần của hình nón là

\(\pi x\sqrt {{x^2} + {y^2}}  + \pi {x^2},\)

Theo gia thiết ta có

\(\eqalign{  & \pi x\sqrt {{x^2} + {y^2}}  + \pi {x^2} = \pi {a^2}  \cr  &  \Leftrightarrow x\sqrt {{x^2} + {y^2}}  + {x^2} = {a^2}  \cr  &  \cr} \)

\( \Leftrightarrow x\sqrt {{x^2} + {y^2}}  = {a^2} - {x^2}\) (điều kiện x < a)

\(\eqalign{  &  \Leftrightarrow {x^2}({x^2} + {y^2}) = {a^4} + {x^4} - 2{a^2}{x^2}  \cr  &  \Leftrightarrow {x^2}{y^2} = {a^4} - 2{a^2}{x^2} \Leftrightarrow {x^2} = {{{a^4}} \over {{y^2} + 2{a^2}}} \cr} \)

Khi đó thể tích khối nón là

\(V = {1 \over 3}\pi {{{a^4}} \over {{y^2} + 2{a^2}}}.y = {{\pi {a^4}} \over 3}.{y \over {{y^2} + 2{a^2}}}.\)

Từ đó V đạt giá trị lớn nhất khi và chỉ khi \({{{y^2} + 2{a^2}} \over y}\) đạt giá trị nhỏ nhất.

Ta có \({{{y^2} + 2{a^2}} \over y} = y + {{2{a^2}} \over y} \ge 2\sqrt {y.{{2{a^2}} \over y}}  = 2\sqrt 2 a.\)

Vậy V đạt giá trị lớn nhất khi và chỉ khi \(y = {{2{a^2}} \over y},\) tức là \(y = a\sqrt 2 \), lúc đó \(x = {a \over 2}.\)

Sachbaitap.com