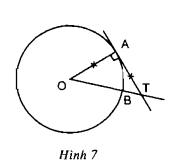
Bài 4. 5, 6, 7, 8, 9 trang 69, 70 SGK Toán 9 tập 2 - Luyện tập

Bài 4 trang 69 SGK Toán lớp 9 tập 2

Câu hỏi:

 Xem hình 7. Tính số đo góc ở tâm \(AOB\) và số đo cung lớn \(AB\)

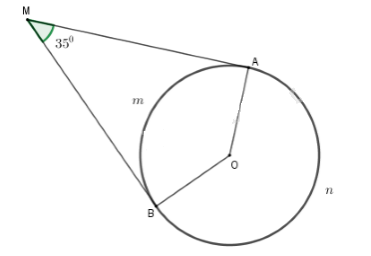
Phương pháp: 

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

Số đo của cung lớn bằng hiệu giữa \({360^o}\) và số đo của cung nhỏ (có chung hai mút với cung lớn)

Số đo của nửa đường tròn bằng \({180^o}\)

Lời giải: 

Ta có \(OA = AT\) (gt) và \(\widehat {OAT} = 90^0\) nên  \(∆AOT\) là tam giác vuông cân tại \(A\), vậy \(\widehat{AOB}=45^0\). 

\(\Rightarrow\) Số đo cung nhỏ \(\overparen{AB} =\widehat{AOB}= 45^0\). Do đó số đo cung lớn \(\overparen{AB}\) là: \(360^0-45^0=315^0\) 

Bài 5 trang 69 SGK Toán lớp 9 tập 2

Câu hỏi:

 Hai tiếp tuyến của đường tròn \((O)\) tại \(A\) và \(B\) cắt nhau tại \(M\). Biết \(\widehat{AMB}=35^0\).

a) Tính số đo của góc ở tâm tạo bởi hai bán kính \(OA, OB\).

b) Tính số đo mỗi cung \(AB\) (cung lớn và cung nhỏ).

Phương pháp:

a) Sử dụng tính chất tia tiếp tuyến

Sử dụng định lý: Tổng bốn góc trong tứ giác bằng \(360^\circ \)

b) Sử dụng:

Số đo cung nhỏ bằng số đo góc ở tâm chắn cung đó

Số đo cung lớn bằng \(360^\circ \) trừ số đo cung nhỏ (có chung hai mút với cung lớn)

Lời giải:

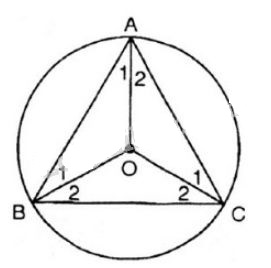
a) Vì \(MA,MB\) là hai tiếp tuyến của \(\left( O \right)\) cắt nhau tại \(M\) nên \(\widehat {OAM} = 90^\circ ;\,\widehat {MBO} = 90^\circ \) 

Xét tứ giác \(OBMA\) có \(\widehat {OAM} + \widehat {OBM} + \widehat {AMB} + \widehat {AOB} = 360^\circ \) (định lý tổng các góc của tứ giác)

Hay \(90^\circ  + 90^\circ  + 35^\circ  + \widehat {AOB} = 360^\circ \\ \Rightarrow \widehat {AOB} = 145^\circ .\)

Vậy số đo của góc ở tâm tạo bởi hai bán kính \(OA, OB\) là:\( \widehat {AOB} =145^0\)

b) Từ \(\widehat {AOB} = {145^0}\). \(\Rightarrow\) Số đo cung nhỏ \(\overparen{AB}\) là \(145^0\) và số đo cung lớn \(\overparen{AB}\) là: \({360^0} - {145^0} = {215^0}\) 

Bài 6 trang 69 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho tam giác đều \(ABC\). Gọi \(O\) là tâm của đường tròn đi qua ba đỉnh \(A, B, C\).

a) Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính \(OA, OB, OC\).

b) Tính số đo các cung tạo bởi hai trong ba điểm \(A, B, C\).

Phương pháp:

Sử dụng:

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

Số đo của cung lớn bằng hiệu giữa \({360^o}\) và số đo của cung nhỏ (có chung hai mút với cung lớn)

Lời giải:

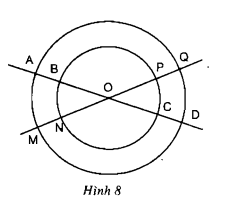
a) Ta có: \(\widehat A = \widehat B = \widehat C = {60^0}\) (gt)

Tâm \(O\) của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều \(ABC\).

Nên \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}} = {30^0}\) 

Suy ra:  \(\widehat {AOB} = {180^0} - \widehat {{A_1}} - \widehat {{B_1}} = {180^0} - {30^0} - {30^0} = {120^0}\)

Tương tự ta suy ra: \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\)

b) Từ \(\widehat {AOB} = \widehat {BOC} = \widehat {COA} = {120^0}\) ta suy ra:

\(sđ\overparen{AB}=sđ\overparen{CA}=sđ\overparen{CB}\) \(= 120^0\)

\(sđ\overparen{ABC}=sđ\overparen{BCA}=sđ\overparen{CAB}\) \(=360^0- 120^0=240^0\)

Bài 7 trang 69 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho hai đường tròn cùng tâm \(O\) với bán kính khác nhau. Hai đường thẳng đi qua \(O\) cắt hai đường tròn đó tại các điểm \(A, B, C, D, M, N, P, Q\) (h.8)

a)Em có nhận xét gì về số đo của các cung \(AM, CP, BN, DQ\).

b) Hãy nêu tên các cung nhỏ bằng nhau.

c) Hãy nêu tên hai cung lớn bằng nhau.

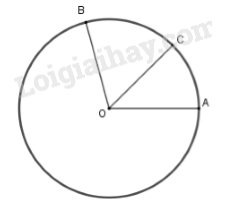
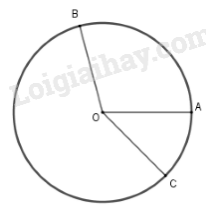
Phương pháp:

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

Số đo của cung lớn bằng hiệu giữa \({360^o}\) và số đo của cung nhỏ (có chung hai mút với cung lớn)

Hai cung bằng nhau có số đo bằng nhau.

Lời giải:

a) Các cung nhỏ \(\overparen{AM}, \overparen{CP}, \overparen{BN}, \overparen{DQ}\) có cùng số đo (cùng bằng góc BON)

b) \(\overparen{AM}\) = \(\overparen{DQ}\); \(\overparen{BN}\) = \(\overparen{PC}\); \(\overparen{AQ}\) =\(\overparen{ MD}\); \(\overparen{BP}\) =\(\overparen{NC}\).

c) Các cung lớn bằng nhau:

\(\overparen{AMDQ} = \overparen{MAQD}\); \(\overparen{BNCP} = \overparen{NBPC}\)

Chú ý:

+ Phân biệt "so sánh hai cung" và "so sánh số đo hai cung":

Ta chỉ so sánh được hai cung trong cùng một đường tròn hoặc trong hai đường tròn bằng nhau.

So sánh số đo hai cung : luôn so sánh được

+ Ở câu c, ta có thể chọn 2 cung lớn bằng nhau khác, chẳng hạn: \(\overparen{AQDM} = \overparen{DMAQ}\); \(\overparen{BPCN} = \overparen{CNBP}\)

Bài 8 trang 70 SGK Toán lớp 9 tập 2

Câu hỏi:

 Mỗi khẳng định sau đây đúng hay sai? Vì sao?

a) Hai cung bằng nhau thì có số đo bằng nhau.

b) Hai cung có số đo bằng nhau thì bằng nhau.

c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn hơn.

d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.

Phương pháp:

So sánh hai cung:

Ta chỉ so sánh hai cung trong một đường tròn hay trong hai đường tròn bằng nhau: Khi đó:

- Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.

- Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

Lời giải:

Ta chỉ so sánh hai cung trong một đường tròn hay trong hai đường tròn bằng nhau

a) Đúng 

Chú ý: Khi ta nói hai cung bằng nhau, nghĩa là hai cung này so sánh được (tức chúng cùng nằm trong một đường tròn hoặc trong hai đường tròn bằng nhau). Do đó, theo cách so sánh hai cung đã biết thì hai cung bằng nhau thì số đo bằng nhau. 

b) Sai vì không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.

c) Sai vì không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.

d) Đúng vì ta chỉ so sánh hai cung trong một đường tròn hay trong hai đường tròn bằng nhau. Khi đó, trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn

Bài 9 trang 70 SGK Toán lớp 9 tập 2

Câu hỏi:

Trên đường tròn tâm \(O\) lấy ba điểm \(A, B, C\) sao cho \(\widehat{AOB}  = 100^0\), sđ cung \(\overparen{AC} = 45^0\). Tính số đo của cung nhỏ \(\overparen{BC}\) và cung lớn \(\overparen{BC}\). (Xét cả hai trường hợp: điểm \(C\) nằm trên cung nhỏ \(\overparen{AB}\), điểm \(C\) nằm trên cung lớn \(\overparen{AB}\)).

Phương pháp: 

Sử dụng:

+ Nếu \(C\) là một điểm nằm trên cung \(AB\)  thì  số đo cung \(AB = \)số đo cung \(AC + \) số đo cung \(BC\).

+ Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

+ Số đo của cung lớn bằng hiệu giữa \({360^o}\) và số đo của cung nhỏ (có chung hai mút với cung lớn)

Lời giải:

TH1: Điểm \(C\) nằm trên cung nhỏ \(\overparen{AB}\)

Số đo cung nhỏ BC là \(sđ \overparen{BC} = sđ \overparen{AB}-sđ \overparen{AC}= 100^0 – 45^0 = 55^0\)

Số đo cung lớn \(\overparen{BC} = 360^0 – 55^0 = 305^0\) 

TH2: Điểm \(C\) nằm trên cung lớn \(\overparen{AB}\)

Số đo cung nhỏ BC là \(sđ \overparen{BC} = sđ \overparen{AB}+sđ \overparen{AC}= 100^0 + 45^0= 145^0\)

Số đo cung lớn \(\overparen{BC} = 360^0 – 145^0 = 215^0\) 

Sachbaitap.com