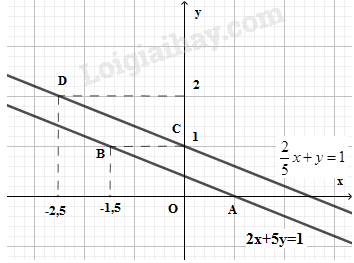
Bài 40, 41, 42, 43, 44, 45, 46 trang 27 SGK Toán 9 tập 2 - Ôn tập chương III - Hệ hai phương trình bậc nhất hai ẩn

Bài 40 trang 27 SGK Toán lớp 9 tập 2

Câu hỏi:

Giải các hệ phương trình sau và minh họa hình học kết quả tìm được:

a) \(\left\{ \matrix{2{\rm{x}} + 5y = 2 \hfill \cr {\displaystyle{2 \over 5}}x + y = 1 \hfill \cr} \right.\)

b) \(\left\{ \matrix{0,2{\rm{x}} + 0,1y = 0,3 \hfill \cr 3{\rm{x}} + y = 5 \hfill \cr} \right.\)

c) \(\left\{ \matrix{{\displaystyle{3 \over 2}}x - y = {\displaystyle{1 \over 2}} \hfill \cr 3{\rm{x}} - 2y = 1 \hfill \cr} \right.\) 

Phương pháp:

Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số để tìm nghiệm

Minh họa hình học: Tức là ta biểu thị 2 đường thẳng trên cùng hệ trục tọa độ. 

Lời giải:

a) Giải hệ phương trình: 

\(\left\{ \matrix{
2{\rm{x}} + 5y = 2 \hfill \cr 
{\displaystyle{2 \over 5}}x + y = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2{\rm{x}} + 5y = 2 \hfill \cr 
- 2{\rm{x}} - 5y = - 5 \hfill \cr} \right.\)

Cộng vế với vế của hai phương trình trong hệ trên, ta được: \(2x + 5y +(-2x-5y)= 2-5 \) 

\( \Leftrightarrow 0 =  - 3\)  (vô lý)

Vậy hệ đã cho vô nghiệm.

Minh họa hình học kết quả tìm được:

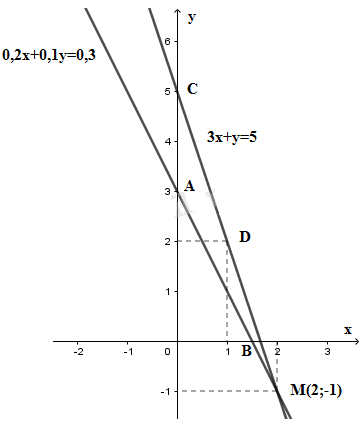
- Vẽ đồ thị hàm số \(2x + 5y = 2\).

Cho \(y = 0 ⇒  x = 1\). Ta xác định được điểm \(A(1; 0)\)

Cho \(y = 1 ⇒ x = -1,5\). Ta xác định được điểm \(B(-1,5; 1)\).

Đồ thị hàm số \(2x + 5y = 2\) là đường thẳng đi qua hai điểm A và B

-Vẽ đồ thị hàm số  \({\displaystyle{2 \over 5}}x + y = 1 \Leftrightarrow 2{\rm{x}} + 5y = 5\)

Cho \(x = 0 ⇒ y = 1\). Ta xác định được điểm \(C(0; 1)\)

Cho \(y = 2 ⇒ x = -2,5\). Ta xác định được điểm \(D(-2,5; 2)\)

Đồ thị hàm số \({\displaystyle{2 \over 5}}x + y = 1\) là đường thẳng đi qua hai điểm C và D.

Kết luận: Đồ thị hai hàm số trên song song. Điều này chứng tỏ rằng hệ phương trình vô nghiệm.

b)  

Giải hệ phương trình:  

\(\left\{ \matrix{
0,2{\rm{x}} + 0,1y = 0,3 \hfill \cr 
3{\rm{x}} + y = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
- 2{\rm{x}} - y = - 3 \hfill \cr 
3{\rm{x}} + y = 5 \, (2) \hfill \cr} \right.\)

Cộng vế với  vế của hai phương trình trên, ta được \(-2x-y+3x+y=-3+5\) \( \Leftrightarrow x = 2\)

Thế \(x = 2\) vào phương trình (2), ta được: \(6 + y = 5 ⇔ y = -1\)

Vậy nghiệm của hệ phương trình là \((x;y)=(2;-1)\)

Minh họa hình học:

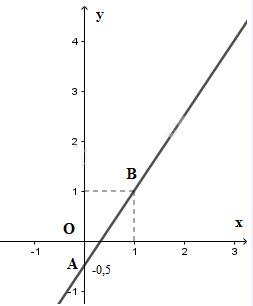
- Đồ thị hàm số \(0,2x + 0,1y = 0,3\) là một đường thẳng đi qua hai điểm:

\(A( 0; 3)\) và \(B(1,5; 0)\)

- Đồ thị hàm số \(3x + y = 5\) là một đường thẳng đi qua hai điểm \(C( 0;  5)\) và \(D( 1; 2)\)

- Đồ thị hai hàm số trên cắt nhau tại điểm: \(M( 2;  -1)\).

Vậy \((2; -1)\) là một nghiệm của hệ phương trình.

c) 

Giải hệ phương trình:

\(\left\{ \matrix{
{\displaystyle{3 \over 2}}x - y = {\displaystyle{1 \over 2}} \hfill \cr 
3{\rm{x}} - 2y = 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
- 3{\rm{x}} + 2y = - 1 \hfill \cr 
3{\rm{x}} - 2y = 1 \hfill \cr} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}3x - 2y = 1\\ - 3x + 2y + 3x - 2y =  - 1 + 1\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}2y = 3x - 1\\0 = 0\left( {luôn \, đúng} \right)\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}y = \dfrac{3}{2}x - \dfrac{1}{2}\\x \in \mathbb{R}\end{array} \right.\)

Vậy hệ phương trình đã cho có vô số nghiệm.

Nghiệm tổng quát là \(\left( {x;{\displaystyle{3 \over 2}}x - {\displaystyle{1 \over 2}}} \right)\)  với \(x ∈ R\)

Minh họa hình học 

- Đồ thị hàm số \(\dfrac{3}{2}x - y = \dfrac{1}{2}\)  và đồ thị hàm số \(3x - 2y = 1\) cùng là một đường thẳng đi qua hai điểm \(A(0;  - {\displaystyle{1 \over 2}})\) và \(B(1;1)\) nên hai đường thẳng này trùng nhau. Vậy hệ phương trình có vô số nghiệm.

Bài 41 trang 27 SGK Toán lớp 9 tập 2

Câu hỏi:

Giải các hệ phương trình sau:

a) \(\left\{ \matrix{x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1 \hfill \cr \left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1 \hfill \cr} \right.\)

b) \(\left\{ \begin{array}{l}\dfrac{{2x}}{{x + 1}} + \dfrac{y}{{y + 1}} = \sqrt 2 \\\dfrac{x}{{x + 1}} + \dfrac{{3y}}{{y + 1}} =  - 1\end{array} \right.\)

Lời giải: 

a) 

\(\left\{ \matrix{
x\sqrt 5 - \left( {1 + \sqrt 3 } \right)y = 1(1) \hfill \cr 
\left( {1 - \sqrt 3 } \right)x + y\sqrt 5 = 1(2) \hfill \cr} \right.\) 

Ta giải hệ phương trình bằng phương pháp thế:

Từ (1) ta có  \(x = \displaystyle{{\left( {1 + \sqrt 3 } \right)y + 1} \over {\sqrt 5 }}(3)\)

Thế (3) vào (2), ta được:  

\(\eqalign{
& \left( {1 - \sqrt 3 } \right)\left[ {{{\left( {1 + \sqrt 3 } \right)y + 1} \over {\sqrt 5 }}} \right] + y\sqrt 5 = 1 \cr 
& \Leftrightarrow \left( {1 - \sqrt 3 } \right)\left( {1 + \sqrt 3 } \right)y + \left( {1 - \sqrt 3 } \right) + 5y = \sqrt 5 \cr 
& \Leftrightarrow - 2y + 5y = \sqrt 5 + \sqrt 3 - 1 \cr&\Leftrightarrow y = {{\sqrt 5 + \sqrt 3 - 1} \over 3} \cr} \)

Thế y vừa tìm được vào (3), ta được:

\(\begin{array}{l}
x = \dfrac{{\left( {1 + \sqrt 3 } \right)\left( {\sqrt 5  + \sqrt 3  - 1} \right) + 3}}{{3\sqrt 5 }} = \dfrac{{\sqrt 5  + \sqrt 3  - 1 + \sqrt {15}  + 3 - \sqrt 3  + 3}}{{3\sqrt 5 }}\\
 = \dfrac{{\sqrt 5  + \sqrt {15}  + 5}}{{3\sqrt 5 }} = \dfrac{{\sqrt 5 \left( {1 + \sqrt 3  + \sqrt 5 } \right)}}{{3\sqrt 5 }} = \dfrac{{1 + \sqrt 3  + \sqrt 5 }}{3}
\end{array}\)

Vậy hệ phương trình có nghiệm là: \(\displaystyle\left( {{{\sqrt 5  + \sqrt 3  + 1} \over 3};{{\sqrt 5  + \sqrt 3  - 1} \over 3}} \right)\)

b) 

Giải hệ phương trình: (I) 

\(\left\{ \begin{array}{l}\dfrac{{2x}}{{x + 1}} + \dfrac{y}{{y + 1}} = \sqrt 2 \\\dfrac{x}{{x + 1}} + \dfrac{{3y}}{{y + 1}} =  - 1\end{array} \right.\)

Điều kiện: \(\displaystyle x \ne  - 1;y \ne  - 1\)

Ta giải hệ phương trình bằng phương pháp đặt ẩn phụ.

Đặt \(\displaystyle u = {x \over {x + 1}};v = {y \over {y + 1}}\)

Thay vào hệ (I), ta có hệ mới với ẩn là \(\displaystyle u\) và \(\displaystyle v\) ta được:

\(\displaystyle \left\{ \matrix{
2u + v = \sqrt 2 \,\,(1') \hfill \cr 
u + 3v = - 1 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
2u + v = \sqrt 2 (3) \hfill \cr 
- 2u - 6v = 2(4) \hfill \cr} \right.\)

Cộng (3) và (4) vế theo vế, ta được: \(\displaystyle - 5{\rm{v}} = 2 + \sqrt 2  \Leftrightarrow v = {{ - \left( {2 + \sqrt 2 } \right)} \over 5}\)

Thay \(\displaystyle v = {{ - \left( {2 + \sqrt 2 } \right)} \over 5}\) vào (1’), ta được:

\(\displaystyle 2u + v = \sqrt 2 \Leftrightarrow 2u  = -v+\sqrt 2\)

\(\displaystyle \Leftrightarrow 2u = {{2 + \sqrt 2 } \over 5} + \sqrt 2  \Leftrightarrow 2u = {{2 + \sqrt 2  + 5\sqrt 2 } \over 5} = {{2 + 6\sqrt 2 } \over 5}\)

\(\displaystyle \Leftrightarrow u = {{1 + 3\sqrt 2 } \over 5}\)

Với giá trị của \(\displaystyle u,v\) vừa tìm được, ta thế vào để tìm nghiệm \(\displaystyle x, y\).

Ta có:  

\(\displaystyle \left\{ \matrix{
{x \over {x + 1}} = {{1 + 3\sqrt 2 } \over 5} \hfill \cr 
{y \over {y + 1}} = {{ - 2 - \sqrt 2 } \over 5} \hfill \cr} \right.\)

\(\displaystyle \Leftrightarrow \left\{ \matrix{
x = \left( {x + 1} \right).\left( {{{1 + 3\sqrt 2 } \over 5}} \right) \hfill \cr 
y = \left( {y + 1} \right).{{{ - 2 - \sqrt 2 }  \over 5}} \hfill \cr} \right.\)

\(\displaystyle \Leftrightarrow \left\{ \matrix{
5{\rm{x}} = \left( {x + 1} \right)\left( {1 + 3\sqrt 2 } \right) \hfill \cr 
5y = \left( {y + 1} \right)\left( { - 2 - \sqrt 2 } \right) \hfill \cr} \right.\)

\(\displaystyle \begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
5x = x\left( {3\sqrt 2 + 1} \right) + 3\sqrt 2 + 1\\
5y = y\left( { - 2 - \sqrt 2 } \right) - 2 - \sqrt 2
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
5x - \left( {3\sqrt 2 + 1} \right)x = 3\sqrt 2 + 1\\
5y - \left( { - 2 - \sqrt 2 } \right)y = - 2 - \sqrt 2
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
\left( {4 - 3\sqrt 2 } \right)x = 3\sqrt 2 + 1\\
\left( {7 + \sqrt 2 } \right)y = - 2 - \sqrt 2
\end{array} \right.
\end{array}\)

\(\displaystyle \Leftrightarrow \left\{ \matrix{
x = {{1 + 3\sqrt 2 } \over {4 - 3\sqrt 2 }} \hfill \cr 
y = {{-2 - \sqrt 2 } \over {7 + \sqrt 2 }} \hfill \cr} \right.\) 

\(\displaystyle \begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
x = \dfrac{{\left( {3\sqrt 2 + 1} \right)\left( {4 + 3\sqrt 2 } \right)}}{{\left( {4 - 3\sqrt 2 } \right)\left( {4 + 3\sqrt 2 } \right)}}\\
y = \dfrac{{\left( { - 2 - \sqrt 2 } \right)\left( {7 - \sqrt 2 } \right)}}{{\left( {7 + \sqrt 2 } \right)\left( {7 - \sqrt 2 } \right)}}
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = \dfrac{{ - 22 - 15\sqrt 2 }}{2}\,(tmđk)\\
y = \dfrac{{ - 12 - 5\sqrt 2 }}{{47}}\,(tmđk)
\end{array} \right.
\end{array}\) 

Vậy nghiệm của hệ phương trình là: \(\displaystyle \left( {\dfrac{{ - 22 - 15\sqrt 2 }}{2};\dfrac{{ - 12 - 5\sqrt 2 }}{{47}}} \right)\) 

Bài 42 trang 27 SGK Toán lớp 9 tập 2

Câu hỏi:

Giải hệ phương trình\(\left\{ \matrix{2{\rm{x}} - y = m \hfill \cr 4{\rm{x}} - {m^2}y = 2\sqrt 2 \hfill \cr} \right.\) trong mỗi trường hợp sau:

a) \(m = -\sqrt{2}\) 

b) \(m = \sqrt{2}\)

c) \(m = 1\)

Lời giải:

a) (I) \(\left\{ \matrix{2{\rm{x}} - y = m(1) \hfill \cr 4{\rm{x}} - {m^2}y = 2\sqrt 2 (2) \hfill \cr} \right.\)

Ta có (1) ⇔ \(y = 2x – m\) (3)

Thế (3) vào (2), ta có:

\(4{\rm{x}} - {m^2}\left( {2{\rm{x}} - m} \right) = 2\sqrt 2\)

\(\Leftrightarrow 4.x - 2.m^2 . x + m^3 = 2\sqrt 2\)

 \(\Leftrightarrow 4.x - 2.m^2 . x = 2\sqrt 2 - m^3\)

\( \Leftrightarrow 2\left( {2 - {m^2}} \right)x = 2\sqrt 2  - {m^3}(*)\) 

Với \(m = - \sqrt{2}\). Thế vào phương trình (*), ta được:

\(2(2 – 2)x = 2\sqrt{2} + 2\sqrt{2} ⇔ 0x = 4\sqrt{2}\) (vô lý)

Vậy hệ phương trình đã cho vô nghiệm.

b) 

(I) \(\left\{ \matrix{2{\rm{x}} - y = m(1) \hfill \cr 4{\rm{x}} - {m^2}y = 2\sqrt 2 (2) \hfill \cr} \right.\)

Ta có (1) ⇔ \(y = 2x – m\) (3)

Thế (3) vào (2), ta có:

\(4{\rm{x}} - {m^2}\left( {2{\rm{x}} - m} \right) = 2\sqrt 2\)

\( \Leftrightarrow 2\left( {2 - {m^2}} \right)x = 2\sqrt 2  - {m^3}(*)\) 

Với \(m = \sqrt{2}\). Thế vào phương trình (*), ta được:

\(2(2 – 2)x = 2\sqrt{2} - 2\sqrt{2} ⇔ 0x = 0\) (luôn đúng)

Phương trình trên nghiệm đúng với mọi x ∈ R, khi đó \(y = 2x – \sqrt 2\)

Vậy hệ trình này có vô số nghiệm dạng \((x;2x-\sqrt 2)\) với \(x\in R\). 

c) 

(I) \(\left\{ \matrix{2{\rm{x}} - y = m(1) \hfill \cr 4{\rm{x}} - {m^2}y = 2\sqrt 2 (2) \hfill \cr} \right.\)

Ta có (1) ⇔ \(y = 2x – m\) (3)

Thế (3) vào (2), ta có:

\(4{\rm{x}} - {m^2}\left( {2{\rm{x}} - m} \right) = 2\sqrt 2\)

\( \Leftrightarrow 2\left( {2 - {m^2}} \right)x = 2\sqrt 2  - {m^3}(*)\) 

Với \(m = 1\). Thế vào phương trình (*), ta được:

\(2.(2-1)x = 2\sqrt 2  - 1 \Leftrightarrow 2{\rm{x}} = 2\sqrt 2  - 1\)

\(\Leftrightarrow x = \displaystyle {{2\sqrt 2  - 1} \over 2}\) 

Thay \(x\) vừa tìm được vào (3), ta có: \(y = 2\sqrt{2} – 2\)

Vậy hệ phương trình có một nghiệm duy nhất là: \(\left( \displaystyle {{{2\sqrt 2  - 1} \over 2};2\sqrt 2  - 2} \right)\)

Bài 43 trang 27 SGK Toán lớp 9 tập 2

Câu hỏi:

Hai người ở hai địa điểm A và B cách nhau 3,6km, khởi hành cùng một lúc, đi ngược chiều nhau và gặp nhau ở một địa điểm cách A là 2km. Nếu cả hai cùng giữ nguyên vận tốc như trường hợp trên nhưng người đi chậm hơn xuất phát trước người kia 6 phút thì sẽ gặp nhau ở chính giữa quãng đường. Tính vận tốc của mỗi người.

Phương pháp:

Các bước giải bài toán bằng cách lập phương trình, hệ phương trình:

Bước 1: Lập phương trình (hệ phương trình)

- Chọn ẩn và đặt điều kiện thích hợp cho ẩn

- Biểu diễn các đại lượng chưa biết theo các ẩn và đại lượng đã biết

- Lập phương trình (hệ phương trình) biểu thị sự tương quan giữa các đại lượng.

Bước 2: giải phương trình và hệ phương trình vừa thu được

Bước 3: Kết luận

- Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thỏa mãn điều kiện của ẩn.

- Kết luận bài toán.

Chú ý: +) Nếu hai người đi ngược chiều và xuất phát cùng một lúc thì đến khi gặp nhau thời gian đi của hai người sẽ bằng nhau.

Sử dụng các công thức \(S = v.t\), \(v = \dfrac{S}{t},t = \dfrac{S}{v}\)

Với \(S:\) là quãng đường, \(v:\) là vận tốc, \(t\): thời gian

+) Đổi đơn vị km/phút ra km/h: a km/ phút = a.60 (km/h)

Lời giải:

Gọi vận tốc của người đi từ A là \(x\) (km/phút), vận tốc của người đi từ B là \(y\,\)(km/phút) (ĐK: \(x;y > 0\))

Nếu hai người khời hành cùng lúc thì gặp nhau tại một điểm cách A là 2km nên lúc này quãng đường người từ A đi được là 2km; quãng đường người từ B đi được là \(3,6 - 2 = 1,6km\). 

Khi đó thời gian người từ A đi là \(\dfrac{2}{x}\)  (phút), thời gian người từ B đi là \(\dfrac{1,6}{y}\) (phút).

Vì hai người khời hành cùng lúc và ngược chiều nên đến khi gặp nhau thời gian hai người đi là bằng nhau, nên ta có phương trình \(\dfrac{2}{x} = \dfrac{{1,6}}{y}\)  (1)

Nhận thấy rằng người đi từ B đi chậm hơn người đi từ A (vì khi khởi hành cùng lúc thì quãng đường người từ B đi ít hơn người đi từ A).

Lại có nếu người đi chậm hơn (người đi từ B) xuất phát trước người đi từ A là 6 phút thì hai người gặp nhau ở chính giữa quãng đường nên mỗi người đi được 1,8 km.

Thời gian hai người đi từ A và đi từ B lần lượt là: \(\dfrac{{1,8}}{x};\dfrac{{1,8}}{y}\) (phút) 

Từ đó, ta có phương trình \(\dfrac{{1,8}}{x} + 6 = \dfrac{{1,8}}{y}\)  (2)

Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}\dfrac{2}{x} = \dfrac{{1,6}}{y}\\\dfrac{{1,8}}{x} + 6 = \dfrac{{1,8}}{y}\end{array} \right.\)

Đặt \(\dfrac{1}{x} = u;\dfrac{1}{y} = v\)  ta có hệ sau \(\left\{ \begin{array}{l}2u = 1,6v\\1,8u + 6 = 1,8v\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u = 0,8v\\1,8.0,8v - 1,8v =  - 6\end{array} \right. \\\Leftrightarrow \left\{ \begin{array}{l}v = \dfrac{{50}}{3}\\u = \dfrac{{40}}{3}\end{array} \right.\)

Thay lại cách đặt ta được \(\left\{ \begin{array}{l}\dfrac{1}{x} = \dfrac{{40}}{3}\\\dfrac{1}{y} = \dfrac{{50}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0,075\\y = 0,06\end{array} \right.\)  (TM )

Vậy vận tốc người đi từ A là \(0,075\) km/phút hay 4,5 km/giờ

Vận tốc người đi từ B là 0,06 km/phút hay 3,6 km/giờ.

Bài 44 trang 27 SGK Toán lớp 9 tập 2

Câu hỏi:

Một vật có khối lượng 124 g và thể tích 15 \(c{m^3}\) là hợp  kim của đồng và kẽm. Tính xem trong đó có bao nhiêu gam đồng và bao nhiêu gam kẽm, biết rằng cứ 89 g đồng thì có thể tích là 10cm³ và 7g kẽm có thể tích là 1cm³

Lời giải:

Gọi \(x;y\) lần lượt là số gam đồng và kẽm có trong vật đã cho (ĐK: \(0 < x;y < 124\))

Vì vật có khối lượng 124g nên ta có phương trình \(x + y = 124\)  (1) 

Biết cứ 89g đồng thì có thể tích là \(10c{m^3}\) nên 1g đồng có thể tích là \(\dfrac{{10}}{{89}}\,c{m^3}\)

Suy ra \(x\) gam đồng có thể tích là \(\dfrac{{10}}{{89}}x\,\,\left( {c{m^3}} \right)\)

Biết cứ 7g kẽm thì có thể tích là \(1c{m^3}\) nên 1g kẽm có thể tích là \(\dfrac{1}{7}\,c{m^3}\)

Suy ra \(y\) gam kẽm có thể tích là \(\dfrac{1}{7}y\,\,\left( {c{m^3}} \right)\)

Vì thể tích vật đã cho là \(15\,c{m^3}\) nên ta có phương trình \(\dfrac{{10}}{{89}}x + \dfrac{1}{7}y = 15\)  (2)

Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 124\\\dfrac{{10}}{{89}}x + \dfrac{1}{7}y = 15\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}y = 124 - x\\70x + 89\left( {124 - x} \right) = 15.7.89\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}y = 124 - x\\ - 19x =  - 1691\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}x = 89\\y = 35\end{array} \right.\)  (TM )

Vậy khối lượng đồng và kẽm trong vật đã cho lần lượt là 89g và 35g.

Bài 45 trang 27 SGK Toán lớp 9 tập 2

Câu hỏi:

Hai đội xây dựng làm chung một công việc và dự định hoàn thành trong 12 ngày. Nhưng khi làm chung được 8 ngày thì đội I được điều động đi làm việc khác. Tuy chỉ còn một mình độ II làm việc nhưng do cải tiến cách làm, năng suất của đội II tăng gấp đôi nên họ làm xong phần việc còn lại trong 3,5 ngày. Hỏi với năng suất ban đầu, nếu mỗi đội làm một mình thì phải làm trong bao nhiêu ngày mới xong công việc trên?

Lời giải:

Với năng suất ban đầu, giả sử đội I làm một mình xong công việc trong \(x\) (ngày) và đội II làm một mình xong công việc trong \(y\) (ngày)
Điều kiện: \(x, y > 12\)

Như vậy, mỗi ngày đội I làm được \(\displaystyle{1 \over x}\) công việc và đội II làm được \(\displaystyle{1 \over y}\) công việc.

Hai đội cùng làm sẽ xong trong 12 ngày nên 1 ngày cả hai đội làm được \(\displaystyle {1 \over {12}}\) công việc. Ta có phương trình:

\(\displaystyle{1 \over x} + \displaystyle{1 \over y} = \displaystyle{1 \over {12}}(1)\)

Trong 8 ngày làm chung, cả hai đội làm được \(\left( \displaystyle{{8 \over x} + \displaystyle{8 \over y}} \right)\) công việc. Do năng suất gấp đôi nên đội II mỗi ngày làm được \(\displaystyle{2 \over y}\) công việc và làm xong phần công việc còn lại trong 3,5 ngày nên trong 3,5 ngày này đội II làm được \(3,5.\displaystyle{2 \over y} = \displaystyle{7 \over y}\) công việc. Ta có phương trình: 

\(\left( \displaystyle{{8 \over x} + \displaystyle{8 \over y}} \right)+\displaystyle{7 \over y}=1\Leftrightarrow \displaystyle{8 \over x} + \displaystyle{{15} \over y}=1 \, (2)\)
Từ (1) và (2) ta có hệ phương trình:\(\left\{ \begin{array}{l}\dfrac{1}{x} + \dfrac{1}{y} = \dfrac{1}{{12}}\\\dfrac{8}{x} + \dfrac{{15}}{y} = 1\end{array} \right.\)

Đặt: 

\(\begin{array}{l}
\left\{ \begin{array}{l}
\dfrac{1}{x} = a\\
\dfrac{1}{y} = b
\end{array} \right.\\
\left\{ \begin{array}{l}
a + b = \dfrac{1}{{12}}\\
8a + 15b = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = \dfrac{1}{{12}} - b\\
8\left( {\dfrac{1}{{12}} - b} \right) + 15b = 1
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
a = \dfrac{1}{{12}} - b\\
\dfrac{2}{3} + 7b = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = \dfrac{1}{{12}} - \dfrac{1}{{21}}\\
b = \dfrac{1}{{21}}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a = \dfrac{1}{{28}}\\
b = \dfrac{1}{{21}}
\end{array} \right.\end{array}\) 

\( \Rightarrow \left\{ \begin{array}{l}
\dfrac{1}{x} = \dfrac{1}{{28}}\\
\dfrac{1}{y} = \dfrac{1}{{21}}
\end{array} \right.\) 

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}
x = 28\\
y = 21
\end{array} \right.
\end{array}\)

Vậy \(x = 28\) (nhận) và \(y = 21\) (nhận)

Vậy đội I làm một mình xong công việc trong 28 ngày, đội II làm một mình xong công việc trong 21 ngày.

Bài 46 trang 27 SGK Toán lớp 9 tập 2

Câu hỏi:

Năm ngoái, hai đơn vị sản xuất nông nghiệp thu hoạch được 720 tấn thóc. Năm nay, đơn vị thứ nhất làm vượt mức 15% , đơn vị thứ hai làm vượt mức 12% so với năm ngoái. Do đó cả hai đơn vị thu hoạch được 819 tấn thóc. Hỏi mỗi năm, mỗi đơn vị thu hoạch được bao nhiêu tấn thóc?

Lời giải:

Gọi \(x\) (tấn) và \(y\) (tấn) là số tấn thóc mà đơn vị thứ nhất và đơn vị thứ hai lần lượt thu hoạch được trong năm ngoái.

Điều kiện: \(x > 0; y > 0\)

Theo đề bài ta có:

Năm ngoái, hai đơn vị sản xuất thu hoạch được 720 tấn thóc nên ta có phương trình:

\(x + y = 720\) (1)

Năm nay, đơn vị thứ nhất làm vượt mức 15% nghĩa là đơn vị thứ nhất thu hoạch được: \(x + \displaystyle{{15} \over {100}}x = {{115} \over {100}}x\) (tấn) và đơn vị thứ hai thu hoạch được : \(y + \displaystyle{{12} \over {100}}y = {{112} \over {100}}y\) (tấn). 

Cả hai thu hoạch được 819 tấn, nghĩa là: \(\displaystyle{{115} \over {100}}x + {{112} \over {100}}y = 819\, (2)\) 

Từ (1) và (2) ta có hệ phương trình: 

\(\left\{ \begin{array}{l}x + y = 720\\\dfrac{{115}}{{100}}x + \dfrac{{112}}{{100}}y = 819\end{array} \right.\)

\(\begin{array}{l}
\Leftrightarrow \left\{ \begin{array}{l}
x + y = 720\\
1,15x + 1,12y = 819
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = 720 - y\\
1,15.\left( {720 - y} \right) + 1,12y = 819
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = 720 - y\\
828 - 1,15y + 1,12y = 819
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
x = 720 - y\\
0,03y = 9
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
y = 300\\
x = 720 - 300
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
y = 300\\
x = 420
\end{array} \right.
\end{array}\) 

Vậy \(x = 420\) (nhận) và \(y = 300\) (nhận)

Vậy:  Năm ngoái đơn vị thứ I thu hoạch được 420 tấn thóc, đơn vị thứ II thu hoạch được 300 tấn thóc.

Năm nay đơn vị thứ I thu hoạch được: \(\displaystyle{{115} \over {100}}.420 = 483\) tấn thóc, đơn vị thứ II thu hoạch được \(\displaystyle{{112} \over {100}}.300 = 336\) tấn thóc

Sachbaitap.com