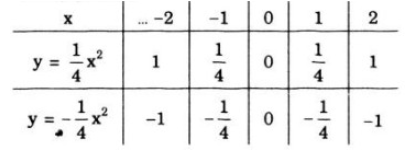
Bài 54, 55, 56, 57, 58, 59 trang 63 SGK Toán 9 tập 2 - Ôn tập chương IV

Bài 54 trang 63 SGK Toán lớp 9 tập 2

Câu hỏi:

Vẽ đồ thị của hàm số \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y =  - {1 \over 4}{x^2}\) trên cùng một hệ trục tọa độ

a) Qua điểm \(B(0; 4)\) kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số \(\displaystyle y = {1 \over 4}{x^2}\) tại hai điểm M và M’. Tìm hoành độ của M và M’.

b) Tìm trên đồ thị của hàm số \(\displaystyle y =  - {1 \over 4}{x^2}\) điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:

- Ước lượng trên hình vẽ:

- Tính toán theo công thức.

Lời giải:

Vẽ đồ thị hàm số: 

* Hàm số \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y =  - {1 \over 4}{x^2}\)

- Tập xác định \(D = R\) 

- Bảng giá trị

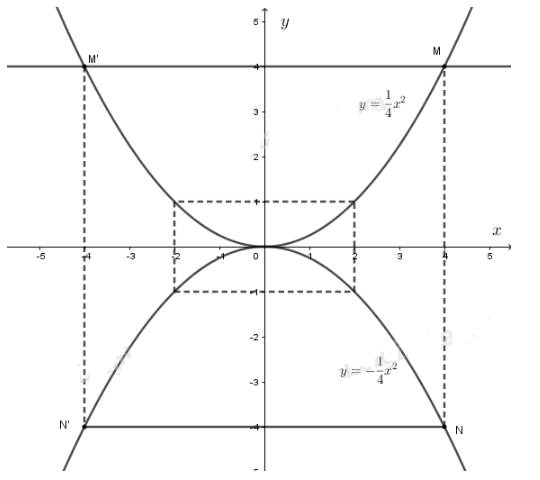
- Đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y =  - {1 \over 4}{x^2}\) là các Parabol có đỉnh là gốc tọa độ O và nhận Oy làm trục đối xứng. Đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}\) nằm trên trục hoành, đồ thị hàm số \(\displaystyle y =  - {1 \over 4}{x^2}\) nằm dưới trục hoành.

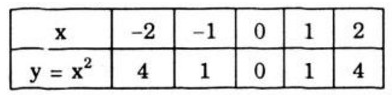
a) Đường thẳng qua \(B(0; 4)\) song song với \(Ox\)  có dạng: y = 4.

Phương trình hoành độ giao điểm của đường thẳng y = 4 và đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}\) là: 

\(\dfrac{1}{4}{x^2} = 4 \Leftrightarrow {x^2} = 16 \Leftrightarrow x =  \pm 4\)

Từ đó ta có hoành độ của \(M\) là \(x = 4\), của \(M'\) là \(x = - 4\).

b) Trên đồ thị hàm số \(\displaystyle y =  - {1 \over 4}{x^2}\) ta xác định được điểm \(N\) và \(N’\) có cùng hoành độ với \(M, M’\). Ta được đường thẳng \(NN'//Ox\)

Tìm tung độ của \(N, N’\)

- Ước lượng trên hình vẽ được tung độ của \(N\) là \(y = - 4\); của \(N’\) là \(y = -4\)

- Tính toán theo công thức:

Điểm \(N(4;y)\).  Thay \(x = 4\) vào \(\displaystyle y =  - {1 \over 4}{x^2}\) nên \(\displaystyle y =  - {1 \over 4}{.4^2} =  - 4\)

Điểm \(N’(-4;y)\). Thay \(x = - 4\) vào  \(\displaystyle y =  - {1 \over 4}{x^2}\) nên \(\displaystyle y =  - {1 \over 4}.{( - 4)^2} =  - 4\)

Vậy tung độ của \(N, N’\) cùng bằng \(-4\). 

Bài 55 trang 63 SGK Toán lớp 9 tập 2

Câu hỏi:

 Cho phương trình \(x^2 – x – 2 = 0\)

a) Giải phương trình

b) Vẽ hai đồ thị \(y = x^2\) và \(y = x + 2\) trên cùng một hệ trục tọa độ.

c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị. 

Lời giải:

a) 

Giải phương trình: \(x^2 – x – 2 = 0\)

\(\Delta = (-1)^2– 4.1.(-2) = 1 + 8 > 0\)

\(\sqrt\Delta= \sqrt9 = 3\) 

\(\Rightarrow {x_1} = -1; {x_2}= 2\) 

b) 

Vẽ đồ thị hàm số

- Hàm số \(y = x^2\)

+ Bảng giá trị:

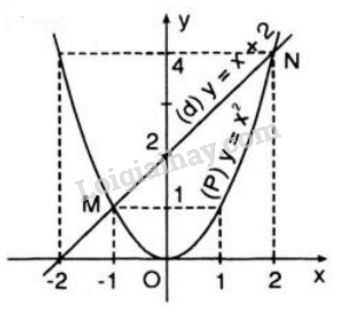
- Hàm số \(y = x + 2\)

+ Cho \(x = 0 ⇒ y = 2\) được điểm \(A(0;2)\)

+ Cho \(x = -2 ⇒ y = 0\) được điểm \(B(-2;0)\)

Đồ thị hàm số: 

c) 

Ta có phương trình hoành độ giao điểm của hai đồ thị là: 

\({x^2} = x + 2 \Leftrightarrow {x^2} - x - 2 = 0\) có \(a - b + c = 1 - \left( { - 1} \right) + \left( { - 2} \right) = 0\) nên có hai nghiệm \({x_1} =  - 1;{x_2} = 2.\)

Điều này chứng tỏ rằng đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là \(x = -1; x= 2\). Hai giá trị này cũng chính là nghiệm của phương trình \(x^2 - x - 2 = 0\) ở câu a).

Bài 56 trang 63 SGK Toán lớp 9 tập 2

Câu hỏi:

Giải các phương trình:

a) \(3{{\rm{x}}^4} - 12{{\rm{x}}^2} + 9 = 0\)

b) \(2{{\rm{x}}^4} + 3{{\rm{x}}^2} - 2 = 0\)

c) \({x^4} + 5{{\rm{x}}^2} + 1 = 0\) 

Lời giải: 

a) 

\(3{{\rm{x}}^4} - 12{{\rm{x}}^2} + 9 = 0\)   

Đặt \(t = {x^2}\left( {t \ge 0} \right)\) 

Ta có phương trình: 

\(\eqalign{
& 3{t^2} - 12t + 9 = 0 \cr 
& \Leftrightarrow {t^2} - 4t + 3 = 0 \cr} \) 

Phương trình có \(a + b + c = 0\) nên có hai nghiệm \({t_1} = 1; {t_2} = 3\) (đều thỏa mãn)

Với \({t_1} = 1 \Rightarrow {x^2} = 1 \Leftrightarrow x =  \pm 1\)

Với \({t_2} = 3 \Rightarrow {x^2} = 3 \Leftrightarrow x =  \pm \sqrt 3\) 

Vậy phương trình đã cho có 4 nghiệm phân biêt.

b) 

 \(2{{\rm{x}}^4} + 3{{\rm{x}}^2} - 2 = 0\)

Đặt \(t = {x^2}\left( {t \ge 0} \right)\)  

Ta có phương trình :

\(\eqalign{
& 2{t^2} + 3t - 2 = 0 \cr 
& \Delta = 9 + 16 = 25 \Rightarrow \sqrt \Delta = 5 \cr 
& \Rightarrow {t_1} = {{ - 3 + 5} \over 4} = {1 \over 2}(TM);{t_2} = - 2(loại) \cr}\)

Với \(\displaystyle t = {1 \over 2} \Rightarrow {x^2} = {1 \over 2} \\\displaystyle \Leftrightarrow x =  \pm \sqrt {{1 \over 2}}  =  \pm {{\sqrt 2 } \over 2}\)

Vậy phương trình đã cho có 2 nghiệm phân biệt.

c) 

\({x^4} + 5{{\rm{x}}^2} + 1 = 0\)    

Đặt \(t = {x^2}\left( {t \ge 0} \right)\) 

Ta có phương trình :

\(t^2 + 5t + 1 = 0\)

\(\Delta = 25 – 4 = 21\)

\(\eqalign{
& \Rightarrow {t_1} = {{ - 5 + \sqrt {21} } \over 2} < 0(loại) \cr 
& {t_2} = {{ - 5 - \sqrt {21} } \over 2} < 0(loại) \cr} \) 

Vậy phương trình vô nghiệm.

Bài 57 trang 63 SGK Toán lớp 9 tập 2

Câu hỏi:

Giải các phương trình:

a)  \(5{{\rm{x}}^2} - 3{\rm{x}} + 1 = 2{\rm{x}} + 11\)

b) \(\displaystyle {{{x^2}} \over 5} - {{2{\rm{x}}} \over 3} = {{x + 5} \over 6}\)

c) \(\displaystyle {x \over {x - 2}} = {{10 - 2{\rm{x}}} \over {{x^2} - 2{\rm{x}}}}\)

d) \(\displaystyle {{x + 0,5} \over {3{\rm{x}} + 1}} = {{7{\rm{x}} + 2} \over {9{{\rm{x}}^2} - 1}}\) 

e) \(2\sqrt 3 {x^2} + x + 1 = \sqrt 3 \left( {x + 1} \right)\)

f) \({x^2} + 2\sqrt 2 x + 4 = 3\left( {x + \sqrt 2 } \right)\) 

Phương pháp: 

Đưa phương trình đã cho về dạng: \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\). Sau đó sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn để tìm nghiệm.

Lời giải: 

a) \(\eqalign{
& 5{{\rm{x}}^2} - 3{\rm{x}} + 1 = 2{\rm{x}} + 11 \cr 
& \Leftrightarrow 5{{\rm{x}}^2} - 5{\rm{x}} - 10 = 0 \cr 
& \Leftrightarrow {x^2} - x - 2 = 0 \cr}\)

Phương trình có \(a – b + c = 1 + 1 – 2 = 0\) nên có 2 nghiệm \({x_1}= -1; {x_2}= 2\)

b) 

\(\eqalign{
& {{{x^2}} \over 5} - {{2{\rm{x}}} \over 3} = {{x + 5} \over 6} \cr 
& \Leftrightarrow 6{{\rm{x}}^2} - 20{\rm{x}} = 5{\rm{x}} + 25 \cr 
& \Leftrightarrow 6{{\rm{x}}^2} - 25{\rm{x}} - 25 = 0 \cr 
& \Delta = {25^2} + 4.6.25 = 1225 \cr 
& \sqrt \Delta = 35 \Rightarrow {x_1} = 5;{x_2} = - {5 \over 6} \cr} \)

Vậy phương trình có 2 nghiệm phân biệt \({x_1} = 5;{x_2} = - {5 \over 6}\)

c)

Điều kiện: \(x \ne \left\{ {0;2} \right\}\)

Ta có \(\dfrac{x}{{x - 2}} = \dfrac{{10 - 2x}}{{{x^2} - 2x}}\)

\( \Leftrightarrow \dfrac{x}{{x - 2}} = \dfrac{{10 - 2x}}{{x\left( {x - 2} \right)}}\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{{x^2}}}{{x\left( {x - 2} \right)}} = \dfrac{{10 - 2x}}{{x\left( {x - 2} \right)}}\\ \Rightarrow {x^2} = 10 - 2x\\ \Leftrightarrow {x^2} + 2x - 10 = 0\end{array}\)

Phương trình trên có \(\Delta ' = {1^2} - 1.\left( { - 10} \right) = 11 > 0\)  nên có hai nghiệm \(\left[ \begin{array}{l}x =  - 1 + \sqrt {11} \\x =  - 1 - \sqrt {11} \end{array} \right.\)  (thỏa mãn)

Vậy phương trình đã cho có hai nghiệm \(x =  - 1 + \sqrt {11} ;x =  - 1 - \sqrt {11} \) .

d) 

\(\displaystyle {{x + 0,5} \over {3{\rm{x}} + 1}} = {{7{\rm{x}} + 2} \over {9{{\rm{x}}^2} - 1}}\) ĐKXĐ: \(x \ne  \pm {1 \over 3}\)

\(\eqalign{
& \Rightarrow {{2{\rm{x}} + 1} \over {3{\rm{x}} + 1}} = {{14{\rm{x}} + 4} \over {9{{\rm{x}}^2} - 1}} \cr 
& \Leftrightarrow \left( {2{\rm{x}} + 1} \right)\left( {3{\rm{x}} - 1} \right) = 14{\rm{x}} + 4 \cr 
& \Leftrightarrow 6{{\rm{x}}^2} + x - 1 = 14{\rm{x}} + 4 \cr 
& \Leftrightarrow 6{{\rm{x}}^2} - 13{\rm{x}} - 5 = 0 \cr 
& \Delta = {( - 13)^2} - 4.6.( - 5) = 289 \cr 
& \sqrt \Delta = \sqrt {289} = 17 \cr 
& \Rightarrow {x_1} = {5 \over 2}(TM) \cr 
& {x_2} = - {1 \over 3}(loại) \cr} \)

Vậy phương trình đã cho có 1 nghiệm duy nhất: \(\displaystyle {x} = {5 \over 2}\)

e) 

\(\begin{array}{l}
2\sqrt 3 {x^2} + x + 1 = \sqrt 3 \left( {x + 1} \right)\\
 \Leftrightarrow 2\sqrt 3 {x^2} - \left( {\sqrt 3  - 1} \right)x + 1 - \sqrt 3 
\end{array}\)

\(\begin{array}{l}
\Delta  = {\left( {\sqrt 3  - 1} \right)^2} - 8\sqrt 3 \left( {1 - \sqrt 3 } \right)\\
\Delta  = 3 - 2\sqrt 3  + 1 - 8\sqrt 3  + 24\\
 = 28 - 10\sqrt 3 \\
 = {5^2} - 2.5.\sqrt 3  + {\left( {\sqrt 3 } \right)^2}\\
 = {\left( {5 - \sqrt 3 } \right)^2}
\end{array}\)

\(\begin{array}{l}
{x_1} = \dfrac{{\sqrt 3  - 1 - 5 + \sqrt 3 }}{{4\sqrt 3 }} = \dfrac{{1 - \sqrt 3 }}{2}\\
{x_2} = \dfrac{{\sqrt 3  - 1 + 5 - \sqrt 3 }}{{4\sqrt 3 }} = \dfrac{{\sqrt 3 }}{3}
\end{array}\)

Vậy phương trình đã cho có 2 nghiệm phân biệt.

f) 

\(\eqalign{
& {x^2} + 2\sqrt 2 x + 4 = 3\left( {x + \sqrt 2 } \right) \cr 
& \Leftrightarrow {x^2} + \left( {2\sqrt 2 - 3} \right)x + 4 - 3\sqrt 2 = 0 \cr 
& \Delta = 8 - 12\sqrt 2 + 9 - 16 + 12\sqrt 2 = 1 \cr 
& \sqrt \Delta = 1 \cr 
& \Rightarrow {x_1} = {{3 - 2\sqrt 2 + 1} \over 2} = 2 - \sqrt 2 \cr 
& {x_2} = {{3 - 2\sqrt 2 - 1} \over 2} = 1 - \sqrt 2 \cr} \)

Bài 58 trang 63 SGK Toán lớp 9 tập 2

Câu hỏi:

Giải các phương trình

a) \(1,2{{\rm{x}}^3} - {x^2} - 0,2{\rm{x}} = 0\)

b) \(5{{\rm{x}}^3} - {x^2} - 5{\rm{x}} + 1 = 0\)

Lời giải: 

a) 

\(1,2{{\rm{x}}^3} - {x^2} - 0,2{\rm{x}} = 0\)

\( \Leftrightarrow x\left( {1,2{{\rm{x}}^2} - x - 0,2} \right) = 0\) 

\(\Leftrightarrow \left[ \matrix{x = 0 \hfill \cr1,2{{\rm{x}}^2} - x - 0,2 = 0(*) \hfill \cr} \right.\)

Giải (*): \(1,2x^2 – x – 0,2 = 0\)

Ta có: \(a + b + c = 1,2 + (-1) + (-0,2) = 0\)  

Vậy (*) có 2 nghiệm: \(\displaystyle {x_1}= 1\); \(\displaystyle  {x_2} = {{ - 0,2} \over {1,2}} =  - {1 \over 6}\) 

Vậy phương trình đã cho có 3 nghiệm: \(\displaystyle {x_1} = 0;{x_2} = 1;{x_3} =  - {1 \over 6}\)

b) 

\(5{{\rm{x}}^3} - {x^2} - 5{\rm{x}} + 1 = 0\)

\(⇔ x^2(5x – 1) – (5x – 1) = 0\)

\(⇔ (5x – 1)(x^2– 1) = 0\) 

\( \displaystyle \Leftrightarrow \left[ \matrix{5{\rm{x}} - 1 = 0 \hfill \cr {x^2} - 1 = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{x = \dfrac{1}{5} \hfill \cr x = \pm 1 \hfill \cr} \right.\)

Vậy phương trình đã cho có 3 nghiệm: \(\displaystyle {x_1} = {1 \over 5};{x_2} =  - 1;{x_3} = 1\)  

Bài 59 trang 63 SGK Toán lớp 9 tập 2

Câu hỏi:

Giải các phương trình bằng cách đặt ẩn phụ:

a) \(2{\left( {{x^2} - 2{\rm{x}}} \right)^2} + 3\left( {{x^2} - 2{\rm{x}}} \right) + 1 = 0\)

b) \({\left( {x + {1 \over x}} \right)^2} - 4\left( {x + {1 \over x}} \right) + 3 = 0\)

Phương pháp: 

Đặt \({x^2} - 2x = t\) để đưa phương trình đã cho về phương trình bậc hai ẩn \(t.\)

Lời giải: 

a) 

Đặt \({x^2} - 2x = t\), ta thu được phương trình \(2{t^2} + 3t + 1 = 0\)

Phương trình trên có \(a - b + c = 2 - 3 + 1 = 0\) nên có hai nghiệm \(t =  - 1;t =  - \dfrac{1}{2}.\)

+ Với \(t =  - 1 \Rightarrow {x^2} - 2x =  - 1\\ \Leftrightarrow {x^2} - 2x + 1 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} = 0 \Leftrightarrow x = 1\)

+ Với \(t =  - \dfrac{1}{2} \Rightarrow {x^2} - 2x =  - \dfrac{1}{2}\\ \Leftrightarrow {x^2} - 2x + 1 = \dfrac{1}{2} \Leftrightarrow {\left( {x - 1} \right)^2} = \dfrac{1}{2}\)

\( \Leftrightarrow \left[ \begin{array}{l}x - 1 = \dfrac{{\sqrt 2 }}{2}\\x - 1 =  - \dfrac{{\sqrt 2 }}{2}\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{2 + \sqrt 2 }}{2}\\x = \dfrac{{2 - \sqrt 2 }}{2}\end{array} \right.\)

Vậy phương trình đã cho có ba nghiệm \(x = 1;x = \dfrac{{2 + \sqrt 2 }}{2};x = \dfrac{{2 - \sqrt 2 }}{2}\)

b) 

ĐK: \(x \ne 0.\)

Đặt \(x + \dfrac{1}{x} = t\), ta thu được phương trình \({t^2} - 4t + 3 = 0\)

Phương trình trên có \(a + b + c = 1 + \left( { - 4} \right) + 3 = 0\) nên có hai nghiệm \(t = 1;t = 3.\)

+ Với \(t = 1 \Rightarrow x + \dfrac{1}{x} = 1 \Rightarrow {x^2} - x + 1 = 0\) .

Xét \(\Delta  = {\left( { - 1} \right)^2} - 4.1.1 =  - 3 < 0\) nên phương trình vô nghiệm.

+ Với \(t = 3 \Rightarrow x + \dfrac{1}{x} = 3\\ \Rightarrow {x^2} - 3x + 1 = 0\, (*)\) 

Phương trình (*) có \(\Delta  = {\left( { - 3} \right)^2} - 4.1.1 = 5 > 0\) nên có hai nghiệm \(\left[ \begin{array}{l}x = \dfrac{{3 + \sqrt 5 }}{2}\\x = \dfrac{{3 - \sqrt 5 }}{2}\end{array} \right.\) (thỏa mãn)

Vậy phương trình đã cho có hai nghiệm \(x = \dfrac{{3 + \sqrt 5 }}{2};x = \dfrac{{3 - \sqrt 5 }}{2}\) .

Sachbaitap.com