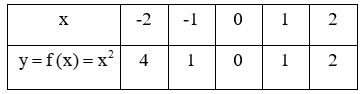
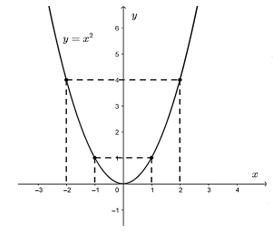
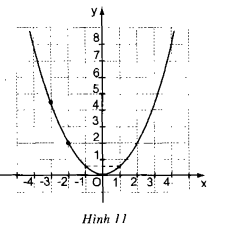
Bài 6, 7, 8, 9, 10 trang 38, 39 SGK Toán 9 tập 2 - Luyện tập

Bài 6 trang 38 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho hàm số \(y = f(x) = {x^2}\).

a) Vẽ đồ thị của hàm số đó.

b) Tính các giá trị \(f(-8); f(-1,3); f(-0,75); f(1,5)\).

c) Dùng đồ thị để ước lượng các giá trị \({(0,5)^2};{( - 1,5)^2};{(2,5)^2}\).

d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số \(\sqrt{3}; \sqrt{7}\).

Lời giải:

a) Ta có bảng giá trị:

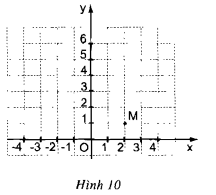
b) Ta có \(y = f(x) = {x^2}\) nên

\(f(-8)=(-8)^2=64.\)

\(f(-1,3)=(-1,3)^2=1,69\).

\(f(-0,75)=(-0,75)^2=0,5625\).

\(f(1,5)=1,5^2=2,25\).

c) Theo đồ thị ta có:

+) Để ước lượng giá trị \((0,5)^2\) ta tìm điểm \(A\) thuộc đồ thị và có hoành độ là \(0,5\). Khi đó tung độ điểm \(A\) chính là giá trị của \((0,5)^2\).

+) Để ước lượng giá trị \((-1,5)^2\) ta tìm điểm \(B\) thuộc đồ thị và có hoành độ là \(-1,5\). Khi đó tung độ điểm \(B\) chính là giá trị của \((-1,5)^2\).

+) Để ước lượng giá trị \((2,5)^2\) ta tìm điểm \(C\) thuộc đồ thị và có hoành độ là \(2,5\). Khi đó tung độ điểm \(C\) chính là giá trị của \((2,5)^2\).

d) Để ước lượng vị trí điểm biểu diễn \(\sqrt 3\) trên trục hoành ta tìm điểm \(D\) thuộc đồ thị và có tung độ là \((\sqrt 3)^2=3\). Khi đó hoành độ điểm \(D\) chính là vị trí biểu diễn của \(\sqrt 3\).

Để ước lượng vị trí điểm biểu diễn \(\sqrt 7\) trên trục hoành ta tìm điểm \(E\) thuộc đồ thị và có tung độ là \((\sqrt 7)^2=7\). Khi đó hoành độ điểm \(E\) chính là vị trí biểu diễn của \(\sqrt 7\).

Bài 7 trang 38 SGK Toán lớp 9 tập 2

Câu hỏi:

Trên mặt phẳng tọa độ (h.10), có một điểm \(M\) thuộc đồ thị của hàm số \(y = a{x^2}\).

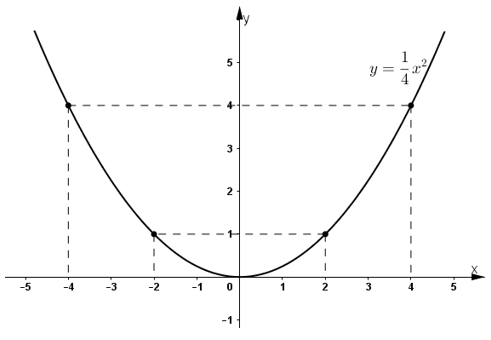
a) Tìm hệ số \(a\)

b) Điểm \(A(4; 4)\) có thuộc đồ thị không ?

c) Hãy tìm thêm hai điểm nữa (không kể điểm O) để vẽ đồ thị.

Lời giải:

a) Vì \(M(2;1)\) thuộc hàm số \(y=ax^2\), thay \(x=2,\ y=1\) vào công thức hàm số, ta có:

\(1=a.2^2 \Leftrightarrow 1=a.4 \Leftrightarrow a=\dfrac{1}{4}\) 

Khi đó , hàm số đã cho có dạng là: \(y=\dfrac{1}{4}x^2\)  (1).

b) Thay \(x=4,\ y=4\) vào công thức hàm số (1), ta được:

\(4=\dfrac{1}{4}.4^2 \) \(\Leftrightarrow 4=4\) (luôn đúng) 

Vậy điểm \(A(4; 4)\) thuộc đồ thị hàm số \(y = \dfrac{1}{4}{x^2}\).

c)  Ta có điểm \(A'(-4;4)\) đối xứng với điểm \(A(4; 4)\) qua trục tung

Điểm \(M'(-2; 1)\) đối xứng với điểm \(M(2; 1)\) qua trục tung 

Vì đồ thị hàm số \(y=\dfrac{1}{2}x^2\) là đường cong đi qua gốc tọa độ, nhận trục \(Oy\) làm trục đối xứng nên \(A',\ M'\) cũng thuộc đồ thị. 

Vẽ đồ thị: 

Bài 8 trang 38 SGK Toán lớp 9 tập 2

Câu hỏi:

Biết rằng đường cong trong hình 11 là một parabol \(y = a{x^2}\).

a) Tìm hệ số \(a\).

b) Tìm tung độ của điểm thuộc parabol có hoành độ \(x = -3\).

c) Tìm các điểm thuộc parabol có tung độ \(y = 8\).

Lời giải:

a) Theo hình vẽ, ta lấy điểm \(A(-2; 2)\) thuộc đồ thị. Thay \(x = -2, y = 2\) vào công thức hàm số \(y=ax^2\), ta được:

 \(2 = a.{( - 2)^2} \Leftrightarrow a = \dfrac{1}{2}\).

Vậy hàm số có dạng: \(y=\dfrac{1}{2}x^2\).

b) Thay \(x=-3\) vào công thức hàm số \(y=\dfrac{1}{2}x^2\), ta được:

\(y=\dfrac{1}{2}.(-3)^2=\dfrac{1}{2}.9=\dfrac{9}{2}.\)

Vậy tung độ cần tìm là \(\dfrac{9}{2}\).

c) Thay \(y=8\) vào công thức đồ thị hàm số, ta được:

\(8 = \dfrac{1}{ 2}{x^2} \Leftrightarrow {x^2} = 16 \Leftrightarrow x =  \pm 4\)

Ta được hai điểm và tọa độ của hai điểm đó là \(M(4; 8)\) và \(M'(-4; 8)\).

Bài 9 trang 39 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho hai hàm số \(y = \dfrac{1 }{3}{x^2}\) và \(y = -x + 6\).

a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm tọa độ các giao điểm của hai đồ thị đó.

Phương pháp:

a) Cách vẽ đồ thị hàm số \(y=ax^2\):

Bước 1: Xác định 2 điểm thuộc đồ thị và các điểm đối xứng của chúng qua \(Oy\).  

Bước 2: Vẽ parabol đi qua gốc \(O(0;0)\) và các điểm trên.

+) Cách vẽ đồ thị hàm số \(y=ax+b\):

Cho \(x=0 \Rightarrow y=b\). Đồ thị hàm số đi qua điểm \(A(0; b)\).

Cho \(y=0 \Rightarrow x =\dfrac{-b}{a}\). Đồ thị hàm số đi qua điểm \(B{\left(\dfrac{-b}{a}; 0 \right)}\)

Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).

b) Tìm tọa độ giao điểm của hai đồ thị hàm số \(y=ax+b\) và \(y=a'x^2\). Ta xét phương trình hoành độ giao điểm: \(ax+b=a'x^2\). Giải phương trình này tìm được hoành độ giao điểm. Thay giá trị đó vào công thức hàm số tìm được tung độ giao điểm.

Lời giải:

a) *Vẽ đồ thị: \(y = \dfrac{1 }{3}{x^2}\).

Bảng giá trị:

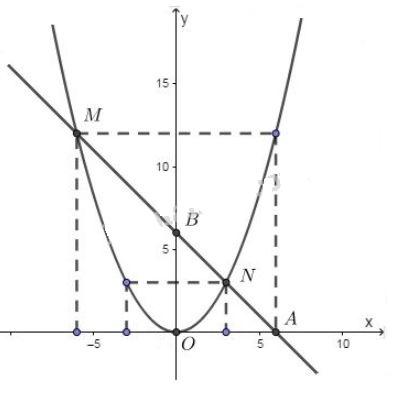
Vẽ parabol đi qua gốc tọa độ và các điểm có tọa độ \(\left( { - 6;12} \right),\left( { - 3;3} \right),\left( {3;3} \right),\left( {6;12} \right)\) ta được đồ thị hàm số \(y = \dfrac{1 }{3}{x^2}\).

*Vẽ đồ thị: \(y = -x + 6\)

- Cho \(x = 0 \Rightarrow  y = 0+6=6\). Đồ thị đi qua \(B(0; 6)\).

- Cho \(y = 0 \Rightarrow  0= -x+6 \Rightarrow x=6\). Đồ thị hàm số đi qua \(A(6; 0)\).

Đồ thị hàm số \(y=-x+6\) là đường thẳng đi qua hai điểm \(A,B\).

Vẽ đồ thị: xem hình bên dưới.

b)  Xét phương trình hoành độ giao điểm:

\(\dfrac{1}{3}x^2=-x+6\)

\(\Leftrightarrow \dfrac{1}{3}x^2 +x -6=0\)

\(\Leftrightarrow x^2+3x-18=0\)

\(\begin{array}{l}\Leftrightarrow{x^2} - 3x + 6x - 18 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + 6\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x + 6} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 6 = 0\\x - 3 = 0\end{array} \right.\end{array}\)

\( \Leftrightarrow \left[ \matrix{
x = -6 \hfill \cr
x = 3 \hfill \cr} \right.\)

Với \(x=3 \Rightarrow y=-3+6=3\). Đồ thị hàm số đi qua điểm \(N(3;3)\).

Với \(x=-6 \Rightarrow y=-(-6)+6=12\). Đồ thị hàm số đi qua điểm \(M(-6;12)\).

Vậy giao điểm của hai đồ thị là  \(N(3;3)\) và \(M(-6;12)\).

Bài 10 trang 39 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho hàm số \(y =  - 0,75{x^2}\). Qua đồ thị của hàm số đó, hãy cho biết khi \(x\) tăng từ \(-2\) đến \(4\) thì giá trị nhỏ nhất và giá trị lớn nhất của \(y\) là bao nhiêu ?

Lời giải:

Ta có bảng giá trị hàm số \(y =  - 0,75{x^2}\) 

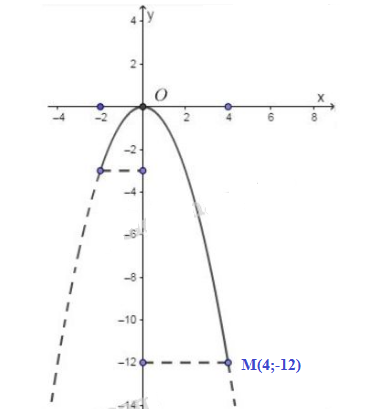
Vẽ parabol đi qua gốc tọa độ và các điểm có tọa độ \(\left( { - 4; - 12} \right);\left( { - 2; - 3} \right);\left( {2; - 3} \right);\left( {4; - 12} \right)\) ta được đồ thị hàm số \(y =  - 0,75{x^2}\)

Vẽ đồ thị: \(y =  - 0,75{x^2}\)

Đồ thị hàm số \(y=-0,75x^2\) với \(x\) từ \(-2\) đến \(4\) là đường cong nét liền trên hình vẽ. 

Ta thấy: Điểm thấp nhất của phần đồ thị nét liền trên hình là điểm \(M(4;-12)\) và điểm cao nhất là gốc tọa độ \(O(0;0)\).

Vậy giá trị lớn nhất của hàm số là \(0\). Giá trị thấp nhất của hàm số là \(-12\). 

Sachbaitap.com