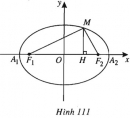
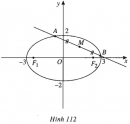
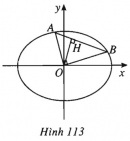
Bài 63 trang 111 SBT Hình học 10 Nâng caoGiải bài tập Bài 63 trang 111 SBT Hình học 10 Nâng cao Tìm những điểm trên elip \((E): \dfrac{{{x^2}}}{9} + {y^2} = 1\) thỏa mãn a) Có bán kính qua tiêu điểm trái bằng hai lần bán kính qua tiêu điểm phải. b) Nhìn hai tiêu điểm dưới một góc vuông. c) Nhìn hai tiêu điểm dưới góc \(60^0\). Giải \({a^2} = 9 \Rightarrow a = 3 ;\) \( {b^2} = 1 \Rightarrow b = 1 ; \) \( {c^2} = {a^2} - {b^2} = 8 \Rightarrow c = 2\sqrt 2 \). Elip \((E)\) có các tiêu điểm: \({F_1}( - 2\sqrt 2 ; 0) , {F_2}(2\sqrt 2 ; 0)\). a) Gọi \(M(x ; y) \in (E)\) là điểm cần tìm. Khi đó: \(\begin{array}{l}M{F_1} = 2M{F_2} \\ \Leftrightarrow a + ex = 2(a - ex) \\ \Leftrightarrow x = \dfrac{a}{{3e}} = \dfrac{{{a^2}}}{{3c}} = \dfrac{3}{{2\sqrt 2 }}.\\M \in (E)\\ \Rightarrow {y^2} = 1 - \dfrac{{{x^2}}}{9}\\ = 1 - \dfrac{9}{{9.8}} = \dfrac{7}{8} \\ \Rightarrow y = \pm \dfrac{{\sqrt 7 }}{{2\sqrt 2 }}.\end{array}\) Có hai điểm cần tìm là \(\left( { \dfrac{3}{{2\sqrt 2 }} ; \pm \dfrac{{\sqrt 7 }}{{2\sqrt 2 }}} \right)\). b) Gọi \(N(x ; y) \in (E)\) là điểm cần tìm. Khi đó: \(\overrightarrow {{F_1}N} = \left( {x + 2\sqrt 2 ; y} \right) , \) \( \overrightarrow {{F_2}N} = \left( {x - 2\sqrt 2 ; y} \right)\). \(\begin{array}{l}\overrightarrow {{F_1}N} \bot \overrightarrow {{F_2}N} \Leftrightarrow \overrightarrow {{F_1}N} .\overrightarrow {{F_2}N} = 0 \\ \Leftrightarrow \left( {x + 2\sqrt 2 } \right)\left( {x - 2\sqrt 2 } \right) + {y^2} = 0\\\Leftrightarrow {x^2} - 8 + {y^2} = 0(1)\\N \in (E) \Rightarrow \dfrac{{{x^2}}}{9} + {y^2} = 1. (2)\end{array}\) Giải (1) và (2) ta được \({x^2} = \dfrac{{63}}{8} \)và \({y^2} = \dfrac{1}{8} \Rightarrow x = \pm \dfrac{{3\sqrt 7 }}{{2\sqrt 2 }}\) và \(y = \pm \dfrac{1}{{2\sqrt 2 }}\). Có bốn điểm cần tìm là : \(\left( { \pm \dfrac{{3\sqrt 7 }}{{2\sqrt 2 }} ; \pm \dfrac{1}{{2\sqrt 2 }}} \right)\). c) Gọi \(P(x ; y) \in (E) \) là điểm cần tìm. Ta có: \(\begin{array}{l}{F_1}{F_2}^2 \\= {F_1}{P^2} + {F_2}{P^2} - 2{F_1}P.{F_2}P.\cos {60^0}\\ = {({F_1}P + {F_2}P)^2} - 2.{F_1}P.{F_2}P - 2{F_1}P.{F_2}P. \dfrac{1}{2}\\= 4{a^2} - 3{F_1}P.{F_2}P \\= 4{a^2} - 3(a + ex)(a - ex)\\ = 4{a^2} - 3({a^2} - {e^2}{x^2}) \\= {a^2} + 3{e^2}{x^2}.\end{array}\) Như vậy \(\begin{array}{l}4{c^2} = {a^2} + 3. \dfrac{{{c^2}}}{{{a^2}}}{x^2} \\ \Rightarrow {x^2} = \dfrac{{(4{c^2} - {a^2}).{a^2}}}{{3{c^2}}}\\ = \dfrac{{(4.8 - 9).9}}{{3.8}} = \dfrac{{69}}{8}\\\Rightarrow x = \pm \dfrac{{\sqrt {69} }}{{2\sqrt 2 }}.\\P \in (E) \Rightarrow {y^2} = 1 - \dfrac{{{x^2}}}{9} \\= 1 - \dfrac{{23}}{{24}} = \dfrac{1}{{24}} \Rightarrow y = \pm \dfrac{1}{{2\sqrt 6 }}.\end{array}\) Có bốn điểm cần tìm với tọa độ là \(\left( { \pm \dfrac{{\sqrt {69} }}{{2\sqrt 2 }} ; \pm \dfrac{1}{{2\sqrt 6 }}} \right)\). Sachbaitap.com
Xem thêm tại đây:
Bài 5. Đường elip.
|

 Tải ngay
Tải ngay