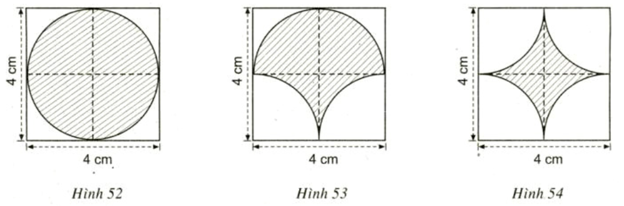
Bài 70, 71, 72, 73, 74, 75, 76 trang 95, 96 SGK Toán 9 tập 2 - Luyện tập

Bài 70 trang 95 SGK Toán lớp 9 tập 2

Câu hỏi:

Vẽ lại ba hình (tạo bởi các cung tròn) dưới đây và tính chu vi mỗi hình (có gạch chéo)

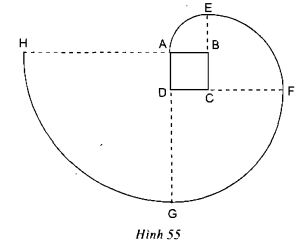
Lời giải: 

- Hình 52: Vẽ hình vuông \(ABCD\) cạnh \(4 cm\). Vẽ hai đường trung trực của các cạnh hình vuông, chúng cắt nhau tại \(O\).

Lấy \(O\) làm tâm vẽ đường tròn bán kính \(2cm\) ta được hình a.

- Hình 53: Vẽ hình vuông như hình a. Lấy \(O\) làm tâm vẽ nửa đường tròn bán kính \(2 cm\) tiếp xúc với các cạnh \(AB, AD, BC\). Lấy \(C,\, \, D\) làm tâm vẽ cung phần tư đường tròn về phía trong hình vuông các cung tròn đã vẽ tạo nên hình b.

- Hình 54: Vẽ hình vuông như hình a. Lấy \(A,B,C,D\) làm tâm vẽ về phía trong hình vuông bốn cung tròn, mỗi cung là phần tư đường tròn. Bốn cung này tạo nên hình c.

Tính chu vi mỗi hình:

- Hình 52: Đường kính đường tròn này là \(4 cm\).

Vậy hình tròn có chu vi là: \(3,14 . 4 = 12,56\) \((cm)\).

- Hình 53: Hình tròn gồm hai cung: một cung là nửa đường tròn, hai cung có mỗi cung là một phần tư đường tròn nên chu vi hình bằng chu vi của hình tròn ở hình 52, tức là \(12,56\) \(cm\).

- Hình 54: Hình gồm bốn cung tròn với mỗi cung tròn là một phần tư đường tròn nên chu vi hình bằng chu vi hình tròn ở hình 52 tức là \(12,56 cm\).                         

Bài 71 trang 96 SGK Toán lớp 9 tập 2

Câu hỏi:

Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là \(B, C, D, A\) theo đúng kích thước đã cho (hình vuông \(ABCD\) dài \(1cm\) ). Nếu cách vẽ đường xoắn \(AEFGH\). Tính độ dài đường xoắn đó.

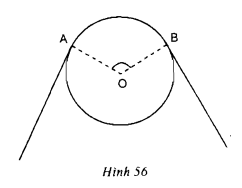
Lời giải:

Cách vẽ: Vẽ hình vuông \(ABCD\) có cạnh dài \(1cm\).

Vẽ \(\dfrac{1}{4}\) đường tròn tâm \(B\), bán kính \(1\) cm, ta có cung \(\overparen{AE}\)

Vẽ \(\dfrac{1}{4}\) đường tròn tâm C, bán kính 2 cm, ta có cung \(\overparen{EF}\)

Vẽ \(\dfrac{1}{4}\) đường tròn tâm D, bán kính 3 cm, ta có cung \(\overparen{FG}\)

Vẽ \(\dfrac{1}{4}\) đường tròn tâm A, bán kính 4 cm, ta có cung \(\overparen{GH}\)

Độ dài đường xoắn:

               \({l_\overparen{AE}}\)= \(\dfrac{1}{4}\) . \(2π.1\)

               \({l_\overparen{EF}}\)= \(\dfrac{1}{4}\) . \(2π.2\)

               \({l_\overparen{FG}}\)= \(\dfrac{1}{4}\) . \(2π.3\)

               \({l_\overparen{GH}}\)= \(\dfrac{1}{4}\) . \(2π.4\)

Vậy: Độ dài đường xoắn là:

\({l_\overparen{AE}}\)+\({l_\overparen{EF}}\)+\({l_\overparen{FG}}\)+\({l_\overparen{GH}}\) 

\(=\dfrac{1}{4}\) .\( 2π (1+2+3+4) = 5π\)

Bài 72 trang 96 SGK Toán lớp 9 tập 2

Câu hỏi:

Bánh xe của một ròng rọc có chu vi là 540mm. Dây cua-roa bao bánh xe theo cung AB có độ dài 200mm. Tính góc AOB (h.56).

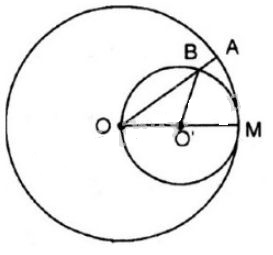
Lời giải:

Chu vi bánh xe là \(C = 540mm\) nên bán kính bánh xe \(R = \dfrac{C}{{2\pi }} = \dfrac{{540}}{{2\pi }}\)\( = \dfrac{{270}}{\pi }\,\left( {mm} \right)\)

Cách 1: Cung \(AB\) có độ dài \(200mm\) và có số đo \(n^\circ \)  nên độ dài  \({l_{\overparen {AB}}} = \dfrac{{\pi Rn}}{{180}} \Rightarrow n = \dfrac{{180.{l_{\overparen {AB}}}}}{{\pi R}}\)\( = \dfrac{{180.200}}{{\pi .\dfrac{{270}}{\pi }}} = \dfrac{{400}}{3} \approx 133\)

Vậy \(\widehat {AOB} \approx 133^\circ \) (góc ở tâm chắn cung \(AB\)). 

Cách 2: Vì góc ở tâm chắn cung và độ dài cung là 2 đại lượng tỉ lệ thuận nên 

\(\frac{\widehat {AOB}}{360^0}=\frac{l_{\overparen {AB}}}{C}\) nên \(\frac{\widehat {AOB}}{360^0}=\frac{200}{540}\)\(\Rightarrow\) \(\widehat {AOB} \approx 133^\circ \)

Bài 73 trang 96 SGK Toán lớp 9 tập 2

Câu hỏi:

Đường tròn lớn của Trái Đất dài khoảng \(40000km\). Tính bán kính Trái Đất.

Lời giải: 

Gọi bán kính Trái Đất là \(R\) thì độ dài đường tròn lớn là: \(C=2\pi R=40000 \,km.\)

 \( \Rightarrow R=\dfrac{40000}{2\pi}≈ 6369 \, (km). \) 

Bài 74 trang 96 SGK Toán lớp 9 tập 2

Câu hỏi:

Vĩ độ của Hà Nội là 20^o01'. Mỗi vòng kinh tuyến của Trái Đất dài khoảng 40 000km. Tính độ dài cung kinh tuyến từ Hà Nội đến xích đạo.

Phương pháp:

+)  Sử dụng công thức tính  chu vi đường tròn có bán kính \(R\) là \(C = 2\pi R \Rightarrow R = \dfrac{C}{{2\pi }}\)

 +) Sử dụng công thức tính độ dài cung \(l = \dfrac{{\pi Rn}}{{180}}\)  với \(n^\circ \) là số đo cung và \(R\) là bán kính đường tròn. 

Lời giải:

Đổi \(20^\circ 01' = 20 + \dfrac{1}{{60}} = {\left( {\dfrac{{1201}}{{60}}} \right)^o}\)

Cách 1:

Vĩ độ của Hà Nội là \(20^001’\) có nghĩa là cung kinh tuyến từ Hà Nội đến xích đạo có số đo là   \({\left( {\dfrac{{1201}}{{60}}} \right)^o}\).

Vậy độ dài cung kinh tuyến từ Hà Nội đến xích đạo là:

\(l = \dfrac{{\pi Rn}}{{180}} = \dfrac{C}{360} = \dfrac{{20000.\dfrac{{1201}}{{60}}}}{{180}} \approx 2224,07km\) 

Cách 2: 

Vì độ dài cung và số đo cung là hai đại lượng tỉ lệ thuận nên \(\dfrac{l}{C}=\dfrac{\frac{1201}{60}}{360}\).

Do đó, \(\dfrac{l}{40000}=\dfrac{\frac{1201}{60}}{360}\) nên \(l=\)\(\dfrac{\frac{1201}{60}}{{360}}. 40000\) \(\approx 2224,07\) (km)

Bài 75 trang 96 SGK Toán lớp 9 tập 2

Câu hỏi:

Cho đường tròn \((O)\), bán kính \(OM\). Vẽ đường tròn tâm \(O'\), đường kính \(OM\). Một bán kính \(OA\) của đường tròn \((O)\) cắt đường tròn \((O')\) ở \(B\).

Chứng minh cung \(MA\) và  cung \(MB\) có độ dài bằng nhau.

Lời giải:

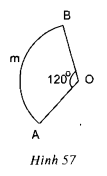
Đặt \(\widehat {MOB} = \alpha \)

\(\Rightarrow \widehat {MO'B} = sđ\overparen{MB} =2\alpha\) (góc nội tiếp và góc ở tâm của đường tròn \((O’)\) cùng chắn cung \(BM\)).

\(\Rightarrow\) Độ dài cung \(MB\) là:

\(\displaystyle {{l_\overparen{MB}}} = {{\pi .O'M.2\alpha } \over {{{180}^0}}} = {{\pi .O'M.\alpha } \over {{{90}^0}}}(1)\)

Xét đường tròn \((O)\), ta có:

\(\widehat{AOM}\) là góc ở tâm chắn cung \(AM \Rightarrow sđ\overparen{AM}= \alpha. \)

\(\Rightarrow\) Độ dài cung \(MA\) là:

\(\displaystyle {{l_\overparen{MA}}} = {{\pi .OM.\alpha } \over {{{180}^0}}} = {{\pi.2 .O'M.\alpha } \over {{{180}^0}}} = {{\pi O'M.\alpha } \over {{{90}^0}}}(2)\)

(Vì \(OM = 2O’M\))

Từ (1) và (2) \(\Rightarrow {l_\overparen{MB}}={l_\overparen{MA}}\).

Bài 76 trang 96 SGK Toán lớp 9 tập 2

Câu hỏi:

Xem hình 57 và so sánh độ dài của cung AmB với độ dài đường gấp khúc AOB.

Lời giải: 

Ta có góc AOB là góc ở tâm chắn cung AmB nên \(sđ \overparen{AmB}=\widehat{AOB}=120^0\)

Ta có độ dài cung \(AmB\) là: \({l_\overparen{AmB}}= \dfrac{\pi R.120}{180}= \dfrac{2\pi R}{3} = 2R.\dfrac{\pi }{3} \approx 2,09.R\) 

Độ dài đường gấp khúc \(AOB\) là \(d.\) 

\(\Rightarrow d = AO + OB = R + R = 2R.\)

Vậy \({l_\overparen{AmB}}>d.\)     

Sachbaitap.com