Bài 7.45 trang 89 Sách bài tập (SBT) Vật lí 11 Nâng caoGiải bài 7.45 trang 89 Sách bài tập (SBT) Vật lí 11 Nâng cao. Một mắt cận về già có điểm cực cận cách mắt 0,4 m và điểm cực viễn cách mắt 1 m. Bài 7.45 trang 89 Sách bài tập (SBT) Vật lí 11 nâng cao Một mắt cận về già có điểm cực cận cách mắt 0,4 m và điểm cực viễn cách mắt 1 m. a) Phải đeo kính \({L_1}\) loại gì, có độ tụ bao nhiêu để có thể thấy rõ vật ở xa vô cực mà mắt không phải điều tiết ? Kính đeo cách mắt 1 cm. b) Để có thể đọc cách mắt 20 cm khi mắt điều tiết tối đa, người ta phải gắn thêm vào phần phía dưới của \({L_1}\) một kính hội tụ \({L_2}\) sao cho mắt nhìn qua cả \({L_1}\) và \({L_2}\). Tính độ tự của kính \({L_2}\). c) Thấu kính \({L_2}\) có hai mặt cong cùng bán kính R, có chiết suất n = 1,5. Tính R. Kính coi như được đeo sát mắt. Giải : a) Kính \({L_1}\) phải đeo sao cho ảnh \({A_1}\) của vật A ở xa vô cực nằm ở điểm cực viễn của mắt. Vậy \(F{'_1}\) của kính trùng với điểm cực viễn trước mắt 1m = 100cm, hay trước kính 100cm - 1cm = 99cm. Vì tiêu điểm ảnh \(F{'_1}\) trước kính nên kính là phân kì. Tiêu cự \({f_1} = - 99cm\), suy ra \({D_1} = {1 \over {{f_1}}} = {1 \over { - 0,99}} \approx - 1dp\) b) Để có thể nhìn rõ vật A (chữ trên sách) thì phải đeo kính L sao cho A cách mắt 20 cm (tức trước kính \(20cm - 1cm = 19cm\)) sẽ cho ảnh \({A_1}\) tại điểm cực cận của mắt, trước mắt \(0,4m = 40cm\) (tức trước kính 39 cm). Sơ đồ tạo ảnh : \(A\mathrel{\mathop{\kern0pt\longrightarrow} Tiêu cự của L là : \(f = {{{\rm{dd}}'} \over {d + d'}} = 37,05cm\) Coi L là hệ hai kính ghép sát từ \({L_1}\) và \({L_2}\), đã biết \(f\) và \({f_1}\), có thể tính \({f_2}\) từ công thức độ tụ : \(\eqalign{ c, Tính R : Từ \({1 \over {{f_2}}} = \left( {n - 1} \right).{2 \over R}\), ta tính được \(R = 26,96cm\). Sachbaitap.com
Xem thêm tại đây:
CHƯƠNG VII: MẮT. CÁC DỤNG CỤ QUANG
|
-
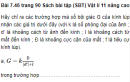
Bài 7.46 trang 90 Sách bài tập (SBT) Vật lí 11 Nâng cao
Giải bài 7.46 trang 90 Sách bài tập (SBT) Vật lí 11 Nâng cao. Hãy chỉ ra các trường hợp mà số bội giác G của kính lúp nhận các giá trị dưới đây (với k là số phóng đại của ảnh ; d’ là khoảng cách từ ảnh đến kính ;
-

Bài 7.47 trang 90 Sách bài tập (SBT) Vật lí 11 Nâng cao
Giải bài 7.47 trang 90 Sách bài tập (SBT) Vật lí 11 Nâng cao. Một mắt không tật có điểm cực cận cách mắt 20 cm, quan sát vật AB qua một kính lúp có tiêu cự f = 2-cm .
-

Bài 7.48 trang 90 Sách bài tập (SBT) Vật lí 11 Nâng cao
Giải bBài 7.48 trang 90 Sách bài tập (SBT) Vật lí 11 Nâng cao. Mắt bình thường có điểm cực cận cách mắt 15 cm, quan sát vật AB qua một kính lúp ở trạng thái không điều tiết.
-

Bài 7.49 trang 91 Sách bài tập (SBT) Vật lí 11 Nâng cao
Giải bài 7.49 trang 91 Sách bài tập (SBT) Vật lí 11 Nâng cao. Nếu thay thấu kính trên bằng một thấu kính phân kì có độ tụ bằng -0,5 dp, thì mắt có thể thấy rõ vật trong khoảng nào ?

 Tải ngay
Tải ngay