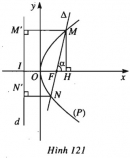
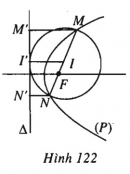
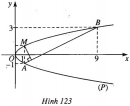
Bài 87 trang 118 SBT Hình học 10 Nâng caoGiải bài tập Bài 87 trang 118 SBT Hình học 10 Nâng cao a) Dùng định nghĩa parabol để lập phương trình của parabol có tiêu điểm \(F(2 ; 1)\) và đường chuẩn \(\Delta : x+y+1=0.\) b) Chứng minh rằng parabol \((P)\) có tiêu điểm \(F\left( { - \dfrac{b}{{2a}} ; \dfrac{{1 - {b^2} + 4ac}}{{4a}}} \right)\) và đường chuẩn \(\Delta : y + \dfrac{{1 + {b^2} - 4ac}}{{4a}} = 0\) có phương trình \(y = a{x^2} + bx + c\). Giải a) Kí hiệu \((P)\) là parabol có tiêu điểm \(F\) và đường chuẩn \(\Delta \). \(\begin{array}{l}M(x ; y) \in (P) \\ \Leftrightarrow MF = d(M ; \Delta ) \\ \Leftrightarrow M{F^2} = {d^2}(M ; \Delta )\\ \Leftrightarrow {(x - 2)^2} + {(y - 1)^2}\\ = \dfrac{{{{(x + y + 1)}^2}}}{2}\\ \Leftrightarrow {x^2} + {y^2} - 2xy - 10x - 6y + 9 = 0.\end{array}\) Vậy \((P)\) có phương trình : \({x^2} + {y^2} - 2xy - 10x - 6y + 9 = 0\). b) Xét điểm tùy ý \(M(x ; y) \in (P)\), hãy biến đổi điều kiện \(MF = d(M ; \Delta )\) qua tọa độ, dẫn đến phương trình \(y = a{x^2} + bx + c\). Sachbaitap.com
Xem thêm tại đây:
Bài 7. Đường parabol
|

 Tải ngay
Tải ngay