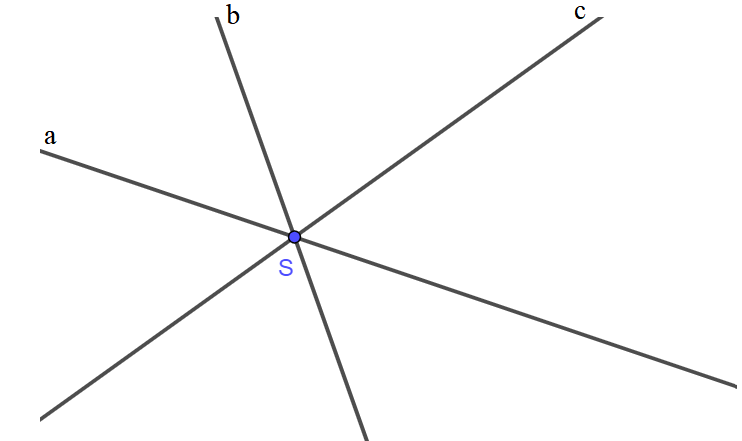
Giải bài 8.7 trang 42 Sách bài tập (SBT) Toán 6 tập 2 - Kết nối tri thức với cuộc sốngBa đường thẳng a, b, c cùng đi qua điểm S; Ba điểm A ∈ a, B ∈ b, C ∈ c thẳng hàng. Câu hỏi: Vẽ hình thể hiện các quan hệ: Ba đường thẳng a,b,c cùng đi qua điểm S; Ba điểm A \( \in \) a, B\( \in \) b, C \( \in \) c thẳng hàng. Phương pháp: Vẽ 3 đường thẳng a,b,c cùng đi qua 1 điểm Lời giải: Cách vẽ: - Vẽ hai đường thẳng a và b cắt nhau tại S. - Vẽ đường thẳng c đi qua điểm S. Ta được ba đường thẳng a, b, c cùng đi qua điểm S (như hình vẽ).
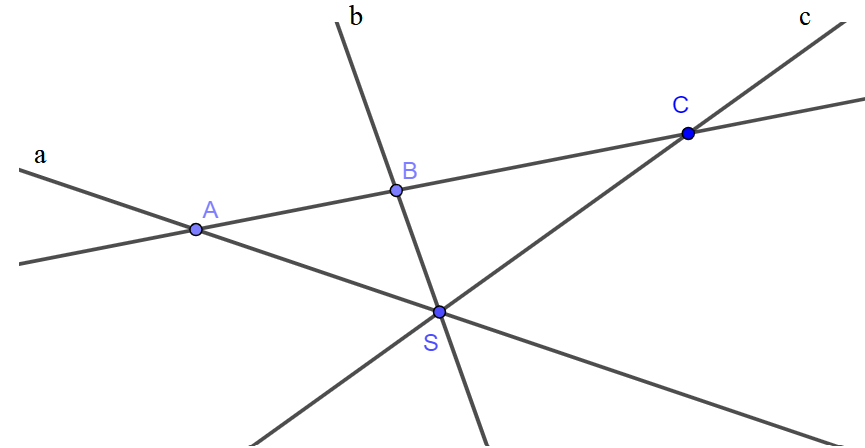
- Lấy điểm A nằm trên đường thẳng a. - Lấy điểm B nằm trên đường thẳng b. - Vẽ đường thẳng đi qua hai điểm A và B cắt đường thẳng c tại điểm C. Ta được ba điểm A ∈ a, B ∈ b, C ∈ c thẳng hàng. Ta có hình vẽ:
Sachbaitap.com
Xem thêm tại đây:
Bài 32: Điểm và đường thẳng - KNTT
|
-

Giải bài 8.8 trang 42 Sách bài tập (SBT) Toán 6 tập 2 - Kết nối tri thức với cuộc sống
Vẽ các đường thẳng AE, BD, BF, EC, AF và DC.
-

Giải bài 8.9 trang 43 Sách bài tập (SBT) Toán 6 tập 2 - Kết nối tri thức với cuộc sống
Xác định các giao điểm I của AE và BD, J của BF và EC, K của AF và DC.
-

Giải bài 8.10 trang 43 Sách bài tập (SBT) Toán 6 tập 2 - Kết nối tri thức với cuộc sống
Kiểm tra xem ba điểm I, J, và K trong bài 8.9 có thẳng hàng không. Em đã kiểm tra bằng cách nào?
-

Giải bài 8.11 trang 43 Sách bài tập (SBT) Toán 6 tập 2 - Kết nối tri thức với cuộc sống
a) Kiểm tra xem hai đường thẳng AB và CD có song song với nhau không. Làm tương tự đối với hai đường thẳng AD và BC. b) Tìm điểm I sao cho ba điểm A, I, C thẳng hàng, ba điểm B, I, D cũng thẳng hàng.

 Tải ngay
Tải ngay