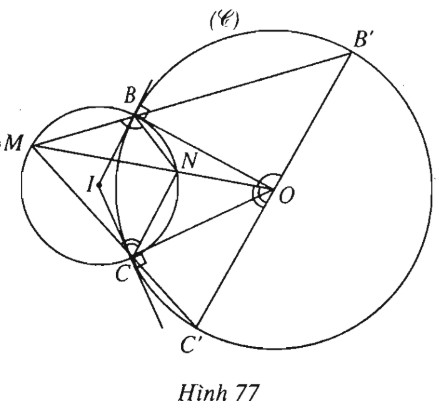
Bài 90 trang 52 SBT Hình học 10 Nâng cao

Cho dây cung $BC$ của đường tròn $C(O ; R) (BC<2R).$

a) Hãy dựng đường tròn tâm $I$ tiếp xúc với $OB$ ở $B$ và tiếp xúc với $OC$ ở $C.$

b) Với mỗi điểm $M$ trên đường tròn $(I)$, kẻ các đường thẳng $MB$ và $MC,$ chúng lần lượt cắt lại đường tròn $(C)$ ở $B’, C’.$

Chứng minh rằng $B’C’$ là đường kính của đường tròn $(C).$

Giải

(h.77).

a) Kẻ hai tiếp tuyến của $(C)$ tại $B$ và $C$, chúng cắt nhau ở $I$. Khi đó, dễ thấy đường tròn tâm $I$ bán kính $r=IB=IC$ thỏa mãn yêu cầu.

b) Kẻ đường thẳng $OM,$ nó cắt đường tròn $(I)$ ở $N$ ($N \ne M$), ta có

$\overrightarrow {OM} .\overrightarrow {ON}  = O{B^2}\,\,( = {\wp _{O/(I)}})$.

Từ đó ta có $\overrightarrow {OM} .\left( {\overrightarrow {OM}  + \overrightarrow {MN} } \right) = {R^2}$, suy ra $O{M^2} - \overrightarrow {OM} .\overrightarrow {MN}  = {R^2}$ hay $\overrightarrow {OM} .\overrightarrow {MN}  = O{M^2} - {R^2}$ $= {\wp _{M/(C)}} = \overrightarrow {MB} .\overrightarrow {MB'}$.

Vậy $N , B, O, B’$ cùng thuộc một đường tròn, suy ra $\widehat {NOB'} = \widehat {NBM}$.

Tương tự ta có $N, C, O, C’$ cùng thuộc một đường tròn, suy ra $\widehat {NOC'} = \widehat {NCM}$.

Do tứ giác $NBMC$ nội tiếp nên $\widehat {NBM} + \widehat {NCM} = {180^0}$.

Từ đó ta có $\widehat {NOB'} + \widehat {NOC'} = {180^0}$. Vậy ba điểm $O, B’, C’$ thẳng hàng hay $B’C’$ là đường kính đường tròn $(C).$

Sachbaitap.com