Bài tập trắc nghiệm trang 38, 39 Sách bài tập (SBT) Giải tích 12Hàm số dạng này có một điểm cực đại tại x = 0 và đồng biến trên khoảng (-∞; b) với b ≤ 0. Vậy hàm số đồng biến trên khoảng (-∞; 0). 1. Hàm số \(y = - {{{x^4}} \over 2} + 1\) đồng biến trên khoảng: A. (-∞; 0) B. (1; +∞) C. (-3; 4) D. (-∞; 1) 2. Với giá trị nào của m, hàm số nghịch biến trên mỗi khoảng xác định của nó? A. \(m = - 1\) B. \(m > 1\) C. \(m \in \left( { - 1;1} \right)\) D. \(m \le - {5 \over 2}\) 3. Các điểm cực tiểu của hàm số là: A. \(x = - 1\) B. \(x = 5\) C. \(x = 0\) D. \(x = 1,\,\,x = 2\) 4. Giá trị lớn nhất của hàm số là: A. 3 B. 2 C. -5 D. 10 5. Cho hàm số A. Hàm số đồng biến trên từng khoảng xác định; B. Hàm số đồng biến trên khoảng (-∞;+∞); C. Hàm số nghịch biến trên từng khoảng xác định; D. Hàm số nghịch biến trên khoảng (-∞;+∞). 6. Tọa độ giao điểm của đồ thị các hàm số \(y = {{{x^2} - 2x - 3} \over {x - 2}}\) và là: A. (2; 2) B. (2; -3) C(-1; 0) D. (3; 1) 7. Số giao điểm của đồ thị hàm số \(y = \left( {x - 3} \right)\left( {{x^2} + x + 4} \right)\) với trục hoành là: A. 2 B. 3 C. 0 D. 1 Hướng dẫn làm bài: 1. Chọn A. Hàm số dạng này có một điểm cực đại tại x = 0 và đồng biến trên khoảng (-∞; b) với b ≤ 0. Vậy hàm số đồng biến trên khoảng (-∞; 0). 2. Chọn D \(\eqalign{ dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (-∞; 2) và (2; +∞) khi \(m \le - {5 \over 2}\). 3. Chọn C Ta có \(y\left( 0 \right) = 2,\,\,\,\,\,\,\,\,\,\,\,\,\,y\left( a \right) = {a^4} + 3{a^2} + 2 \ge 2\) với mọi a ≠ 0 Vậy hàm số có một điểm cực tiểu là x = 0. 4. Chọn B Với mọi x ≠ 0 ta đều có \(y = {4 \over {{x^2} + 2}} \le {4 \over {0 + 2}} = 2\) nên hàm số đạt giá trị lớn nhất khi x = 0 hay \(\mathop {\max y}\limits_R = 2\). 5. Chọn A 6. Chọn C Hàm số \(y = {{{x^2} - 2x - 3} \over {x - 2}}\) không xác định tại x = 2 nên phải loại (A), (B). Thay x = 3 vào hàm số trên, ta được y(3) = 0. Mặt khác, hàm số thứ hai có giá trị là 4 khi x = 3, do đó loại (D). Vậy (C) là khẳng định đúng. 7. Chọn D Vì \({x^2} + x + 4 > 0\) với mọi x nên phương trình \(\left( {x - 3} \right)\left( {{x^2} + x + 4} \right) = 0\) chỉ có một nghiệm là x = 3. Do đó, đồ thị của hàm số đã cho chỉ có một giao điểm với trục hoành. Sachbaitap.com
Xem lời giải SGK - Toán 12 - Xem ngay >> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
Xem thêm tại đây:
Bài tập trắc nghiệm - Chương I
|
-
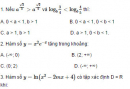
Bài tập trắc nghiệm trang 134, 135 Sách bài tập (SBT) Giải tích 12
Đạo hàm của hàm số y = x(lnx - 1) là:

 Tải ngay
Tải ngay







