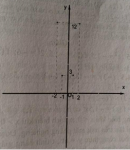
Câu 1 trang 46 Sách bài tập (SBT) Toán 9 tập 2a) Biểu diễn diện tích toàn phần S. Biết rằng hình lập phương có sáu mặt đều là hình vuông. Giả sử x là độ dài của cạnh hình lập phương. a) Biểu diễn diện tích toàn phần S (tức là tổng diện tích của sáu mặt) của hình lập phương qua x. b) Tính các giá trị của S ứng với các giá trị của x cho trong bảng dưới đây rồi điền vào các ô trống.
c) Nhận xét sự tăng, giảm của S khi x tăng. d) Khi S giảm đi 16 lần thì cạnh x tăng hay giảm bao nhiêu lần? e) Tính cạnh của hình lập phương: khi S = \({{27} \over 2}c{m^2}\); khi S = \(5c{m^2}\) Giải a) Hình lập phương 6 mặt đều là hình vuông, diện tích mỗi mặt bằng \({x^2}\) Diện tích toàn phần: \(S = 6{x^2}.\) b)
c) Khi giá trị của x tăng thì giá trị của S tăng. d) Khi S giảm đi 16 lần, gọi giá trị của nó lúc đó là S’ và cạnh hình lập phương là x’. Ta có: \(S' = 6x{'^2}\) (1) \(S = {S \over {16}} = {{6{x^2}} \over {16}} = 6.{{{x^2}} \over {16}} = 6.{\left( {{x \over 4}} \right)^2}\) (2) Từ (1) và (2) suy ra: \(x{'^2} = {\left( {{x \over 4}} \right)^2} \Rightarrow x' = {x \over 4}\) Vậy cạnh của hình vuông giảm đi 4 lần. e) Khi S = \({{27} \over 2}(c{m^2})\) Ta có: \(6{x^2} = {{27} \over 2} \Rightarrow {x^2} = {{27} \over 2}:6 = {9 \over 4}\) Vì x > 0 suy ra: \(x = {3 \over 2}\) (cm) Khi S = 5cm2 \(\eqalign{ \( \Leftrightarrow x = \sqrt {{5 \over 6}} \) (vì x > 0) \( \Rightarrow x = {1 \over 6}\sqrt {30} \) (cm). Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 1. Hàm số bậc hai (a ≠ 0)
|
-
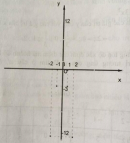
Câu 3 trang 46 Sách bài tập (SBT) Toán 9 tập 2
a) Lập bảng tính các giá trị của y ứng với các giá trị của x.
-
Câu 4 trang 47 Sách bài tập (SBT) Toán 9 tập 2
a) Hãy tính rồi sắp xếp ba giá trị này theo thứ tự từ lớn đến bé.
-
Câu 5 trang 47 Sách bài tập (SBT) Toán 9 tập 2
Hãy xác định hệ số a và đố em biết lần đo nào không cẩn thận.

 Tải ngay
Tải ngay