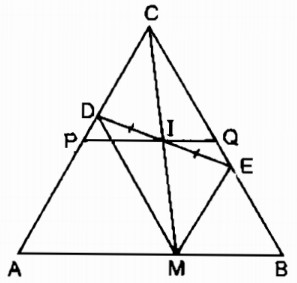
Câu 129 trang 96 Sách bài tập (SBT) Toán 8 tập 1Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào ? Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giác đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào ? Giải:
Gọi giao điểm của AD và BE là C. ∆ ABC có: \(\widehat A = {60^0}\) (vì ∆ ADM đều) \(\widehat B = {60^0}\) (vì ∆ BEM đều) Suy ra: ∆ ABC đều, AC = AB = BC nên điểm C cố định \(\widehat A = \widehat {EMB} = {60^0}\) ⇒ ME // AC (vì có cặp góc đồng vị bằng nhau) hay ME // DC \(\widehat {DMA} = \widehat B = {60^0}\) ⇒ MD // BC (vì có cặp góc đồng vị bằng nhau) hay MD // EC Tứ giác CDME là hình bình hành I là trung điểm của DE nên I là trung điểm của CM Kẻ CH ⊥ AB, IK ⊥ AB ⇒ IK // CH Trong ∆ CHM ta có: CI = IM IK // CH nên IK là đường trung bình của ∆ CHM ⇒ IK = \({1 \over 2}\)CH C cố định ⇒ CH không đổi ⇒ IK =\({1 \over 2}\)CH không thay đổi nên I chuyển động trên đường thẳng song song AB, cách AB một khoảng bằng \({1 \over 2}\)CH. Khi M trùng với A thì I trùng trung điểm P của AC. Khi M trùng với B thì I trùng với trung điểm Q của BC. Vậy khi M chuyển động trên đoạn thẳng AB thì I chuyển động trên đoạn PQ (P là trung điểm của AC, Q là trung điểm của BC) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 10. Đường thẳng song song với một đường thẳng cho trước
|
-
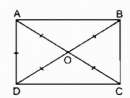
Câu 130 trang 96 Sách bài tập (SBT) Toán 8 tập 1
Hình chữ nhật ABCD có cạnh AD bằng nửa đường chéo AC. Tính góc nhọn tạo bởi hai đường chéo.
-
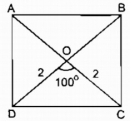
Câu 131 trang 96 Sách bài tập (SBT) Toán 8 tập 1
Dựng hình chữ nhật ABCD, biết đường chéo AC = 4cm, góc tạo bởi hai đường chéo bằng 100°.

 Tải ngay
Tải ngay