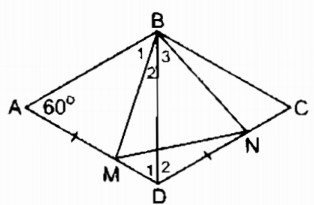
Câu 140 trang 97 Sách bài tập (SBT) Toán 8 tập 1Tam giác BMN là tam giác gì ? Vì sao ? Hình thoi ABCD có \(\widehat A = {60^0}\) . Trên cạnh AD lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = DN. Tam giác BMN là tam giác gì ? Vì sao ? Giải:
Nối BD, ta có: AB = AD (gt) nên ∆ ABD cân tại A mà \(\widehat A = {60^0}\) ⇒ ∆ ABD đều \( \Rightarrow \widehat {ABD} = {\widehat D_1} = {60^0}\) và BD = AB Suy ra: BD = BC = CD ⇒ ∆ CBD đều \( \Rightarrow {\widehat D_2} = {60^0}\) Xét ∆ BAM và ∆ BDN: AB = BD (chứng minh trên) \(\widehat A = {\widehat D_2} = {60^0}\) AM = DN Do đó: ∆ BAM = ∆ BDN (c.g.c) \( \Rightarrow {\widehat B_1} = {\widehat B_3}\) và BM = BN Suy ra: ∆ BMN cân tại B \({\widehat B_2} + {\widehat B_1} = \widehat {ABD} = {60^0}\) Suy ra: \({\widehat B_2} + {\widehat B_3} = \widehat {MBN} = {60^0}\) Vậy ∆ BMN đều Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 11. Hình thoi
|
-
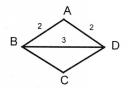
Câu 143 trang 97 Sách bài tập (SBT) Toán 8 tập 1
Dựng hình thoi ABCD, biết cạnh bằng 2cm, một đường chéo bằng 3cm.

 Tải ngay
Tải ngay