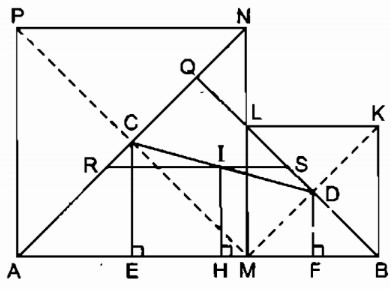
Câu 164 trang 101 Sách bài tập (SBT) Toán 8 tập 1Tính khoảng cách từ I đến AB Cho đoạn thẳng AB = a. Gọi M là một điểm nằm giữa A và B. Vẽ về một phía của AB các hình vuông AMNP, BMLK có tâm theo thứ tự là C, D. Gọi I là trung điểm của CD. a. Tính khoảng cách từ I đến AB b. Khi điểm M di chuyển trên đoạn thẳng AB thì điểm I di chuyển trên đường nào ? Giải:
a. Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB ⇒ CE // DF // IH IC = ID (gt) nên IH là đường trung bình của hình thang DCEF \( \Rightarrow IH = {{DF + CE} \over 2}\) (1) C là tâm hình vuông AMNP ⇒ ∆ CAM là tam giác vuông cân tại C CE ⊥ AM ⇒ CE là đường trung tuyến (tính chất tam giác cân) ⇒ CE = \({1 \over 2}\)AM D là tâm hình vuông BMLK ⇒ ∆ DBM vuông cân tại D DF ⊥ BM ⇒ DF là đường trung tuyến (tính chất tam giác cân) ⇒ DF = \({1 \over 2}\)BM Vậy CE + DF = \({1 \over 2}\)AM + \({1 \over 2}\)BM = \({1 \over 2}\) (AM + BM) = \({1 \over 2}\)AB = \({a \over 2}\) ⇒ IH = \({{{a \over 2}} \over 2} = {a \over 4}\) b. Gọi Q là giao điểm của BL và AN Ta có: AN ⊥ MP (tính chất hình vuông) BL ⊥ MK (tính chất hình vuông) MP ⊥ MK (tính chất hai góc kề bù) Suy ra: BL ⊥ AN ⇒ ∆ QAB vuông cân tại Q cố định. M thay đổi thì I thay đổi luôn cách đoạn thẳng AB cố định một khoảng không đổi bằng \({a \over 4}\) nên I chuyển động trên đường thẳng song song với AB, cách AB một khoảng bằng \({a \over 4}\) Khi M trùng B thì I trùng với S là trung điểm của BQ Khi M trùng với A thì I trùng với R là trung điểm của AQ Vậy khi M chuyển động trên đoạn AB thì I chuyển động trên đoạn thẳng RS song song với AB, cách AB một khoảng bằng \({a \over 4}\) . Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài tập ôn chương I - Tứ giác
|

 Tải ngay
Tải ngay