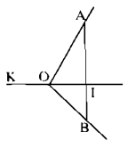
Câu 18 trang 86 Sách Bài Tập (SBT) Toán Lớp 6 tập 2

Ở hình 6, hai tia OI, OK đối nhau. Tia OI cắt đoạn thẳng AB tại I. Biết \(\widehat {K{\rm{O}}A} = {120^O},\widehat {BOI} = {45^O}\). Tính \(\widehat {K{\rm{O}}B},\widehat {AOI},\widehat {BOA}\).

Giải

Vì \(\widehat {K{\rm{O}}B}\) và \(\widehat {BOI}\) kề bù nên:

$$\widehat {K{\rm{O}}B} + \widehat {BOI} = {180^O}$$

Thay \(\widehat {BOI} = {45^O}\) ta có

\(\widehat {K{\rm{O}}B} + {45^O} = {180^O}\)

\( \Rightarrow \) \(\widehat {K{\rm{O}}B} = {180^O} - {45^O} = {135^O}\)

Vì \(\widehat {K{\rm{OA}}}\) và \(\widehat {AOI}\) kề bù nên:

\(\widehat {K{\rm{O}}A} + \widehat {AOI} = {180^O}\)

Thay \(\widehat {K{\rm{O}}A} = {120^O}\) ta có 

\(\eqalign{
& {120^O}\widehat { + AOI} = {180^O} \cr
& \Rightarrow \widehat {AOI} = {180^O} - {120^O} = {60^O} \cr} \)

Vì tia OI nằm giữa hai tia OA và OB nên:

\(\widehat {AOI} + \widehat {I{\rm{O}}B} = \widehat {AOB}\)

Thay \(\widehat {AOI} = {60^O};\widehat {I{\rm{O}}B} = {45^O}\) ta có:

\(\widehat {AOB} = {60^O} + {45^O} = {105^O}\)

Sachbaitap.net