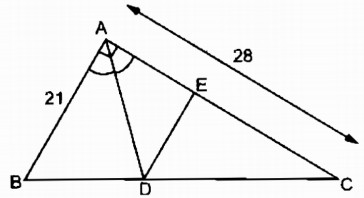
Câu 21 trang 88 Sách bài tập (SBT) Toán 8 tập 2Tính độ dài các đoạn thẳng BD, DC và DE. Cho tam giác vuông ABC (\(\widehat A = {90^0}\)), AB = 21cm, AC = 28cm; đường phân giác góc A cắt BC tại D, đường thẳng qua D và song song với AB, cắt AC tại E a. Tính độ dài các đoạn thẳng BD, DC và DE. b. Tính diện tích tam giác ABD và diện tích tam giác ACD.
Giải:
a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có: \(B{C^2} = A{B^2} + A{C^2} = {21^2} + {28^2} = 1225\) Suy ra: BC = 35 (cm) Vì AD là đường phân giác của \(\widehat {BAC}\) nên: \({{BD} \over {DC}} = {{AB} \over {AC}}\) (tính chất đường phân giác ) Suy ra: \({{BD} \over {BD + DC}} = {{AB} \over {AB + AC}}\) hay \({{BD} \over {BC}} = {{AB} \over {AB + AC}}\) Suy ra: \(BD = {{BC.AB} \over {AB + AC}} = {{35.21} \over {21 + 28}} = 15\) (cm) Vậy DC = BC – BD = 35 – 15 = 20 (cm) Trong tam giác ABC ta có: DE // AB Suy ra: \({{DC} \over {BC}} = {{DE} \over {AB}}\) (Hệ quả định lí Ta-lét ) Suy ra: \(DE = {{DC.AB} \over {BC}} = {{20.21} \over {35}} = 12\) (cm) b. Ta có: \({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}.21.28 = 294(c{m^2})\) Vì ∆ ABC và ∆ ADB có chung đường cao kẻ từ đỉnh A nên: \(\eqalign{ & {{{S_{ADB}}} \over {{S_{ABC}}}} = {{BD} \over {BC}} = {{15} \over {35}} = {3 \over 7} \cr & \Rightarrow {S_{ADB}} = {3 \over 7}{S_{ABC}} = {3 \over 7}.294 = 126(c{m^2}) \cr} \) Vậy \({S_{ADC}} = {S_{ABC}} - {S_{ADB}} = 294 - 126 = 168(c{m^2})\). Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 3. Tính chất đường phân giác của tam giác
|
-
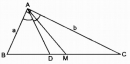
Câu 24 trang 88 Sách bài tập (SBT) Toán 8 tập 2
Tính độ dài các đoạn thẳng BC, BD, DC, AM và DM theo a, b.
-
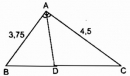
Câu 3.1 trang 89 Sách bài tập (SBT) Toán 8 tập 2
Hãy chọn kết quả đúng (tính chính xác đến chữ số thập phân).

 Tải ngay
Tải ngay