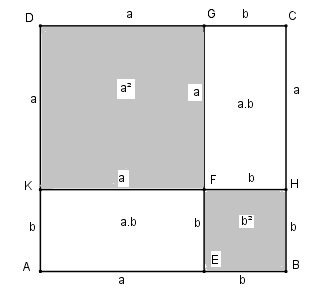
Câu 2.2 trang 159 Sách bài tập (SBT) Toán 8 tập 1Dùng diện tích để chứng tỏ a. Dùng diện tích để chứng tỏ : \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\) b. Dùng diện tích để chứng tỏ : \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)với điều kiện b < a Giải:
a. Dựng hình vuông ABCD có cạnh bằng (a + b ) Trên cạnh AB dựng điểm E sao cho AE = a, EB = b, trên cạnh BC dựng điểm H sao cho BH = b, HC = a, trên cạnh CD dựng điểm G sao cho CG = b, GD = a, trên cạnh DA dựng điểm K sao cho DK = a, KA = b, GE cắt KH tại F. Ta có : diện tích hình vuông ABCD bằng \({\left( {a + b} \right)^2}\) Diện tích hình vuông DKFG bằng \({a^2}\) Diện tích hình chữ nhật AKFE bằng a.b Diện tích hình vuông EBHF bằng \({b^2}\) Diện tích hình chữ nhật HCGF bằng a.b \({S_{ABCD}} = {S_{DKFG}} + {S_{AKFE}} + {S_{EBHF}} + {S_{HCGF}}\) Vậy ta có : \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\) b. Dựng hình vuông ABCD có cạnh bằng a Trên cạnh AB lấy điểm E sao cho BE = b Từ E dựng đường thẳng song song BC cắt CD tại G Ta có: CG = b, CE = ( a – b ), GD = ( a – b ) Trên cạnh AD lấy điểm K sao cho AK = b Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F Ta có: KD = ( a – b ), BH = b Hình vuông ABCD có diện tích bằng \({a^2}\) Hình vuông DKFG có diện tích bằng \({\left( {a - b} \right)^2}\) Hình chữ nhật AEFK có diện tích bằng ( a – b ) b Hình vuông EBHF có diện tích bằng \({b^2}\) Hình chữ nhật HCGF có diện tích bằng ( a – b ).b \({S_{ABCD}} = {S_{DKFG}} + {S_{AEFK}} = {S_{EBHF}} + {S_{HCGF}}\) nên \({\left( {a - b} \right)^2} + \left( {a - b} \right)b + \left( {a - b} \right)b + {b^2} = {a^2}\) \(\Rightarrow {\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\) Sachbaitap.com
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 2. Diện tích hình chữ nhật
|
-
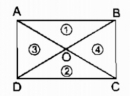
Câu 25 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không ? Vì sao ?
-
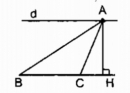
Câu 26 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên một đường thẳng d cố định song song với đường thẳng BC. Chứng minh rằng tam giác ABC luôn có diện tích không đổi.
-
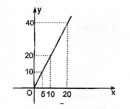
Câu 27 trang 159 Sách bài tập (SBT) Toán 8 tập 1
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A xuống đường thẳng BC.

 Tải ngay
Tải ngay