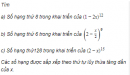Câu 2.27 trang 64 sách bài tập Đại số và Giải tích 11 Nâng caoCho hai đường thẳng a, b song song. Xét tập H có 30 điểm khác nhau, trong đó trên đường thẳng a có 10 điểm và trên đường thẳng b có 20 điểm của H. Có bao nhiêu tam giác mà các đỉnh của nó thuộc tập H? Cho hai đường thẳng a, b song song. Xét tập H có 30 điểm khác nhau, trong đó trên đường thẳng a có 10 điểm và trên đường thẳng b có 20 điểm của H. Có bao nhiêu tam giác mà các đỉnh của nó thuộc tập H? Giải Có hai loại tam giác. Loại 1 : Gồm một điểm trên a và hai điểm trên b. Có \(10.C_{20}^2 = 1900\) tam giác loại 1. Loại 2 : Gồm một điểm trên b và hai điểm trên a. Có \(20.C_{10}^2 = 900\) tam giác loại 2. Vậy tất cả có 1900 + 900 = 2800 tam giác. sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 2: Hoán vị, chỉnh hợp và tổ hợp
|
-
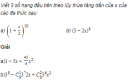
Câu 2.28 trang 65 sách bài tập Đại số và Giải tích 11 Nâng cao
Viết 3 số hạng đầu tiên theo lũy thừa tăng dần của x của các đa thức sau:
-

Câu 2.30 trang 65 sách bài tập Đại số và Giải tích 11 Nâng cao
Viết 4 số hạng đầu tiên theo lũy thừa tăng dần của x của các đa thức sau:

 Tải ngay
Tải ngay