Câu 2.46 trang 67 sách bài tập Đại số và Giải tích 11 Nâng caoMột người say rượu bước bốn bước. Mỗi bước anh ta tiến lên phía trước nửa mét hoặc lùi lại phía sau nửa mét với xác suất như nhau. Tính xác suất để sau bốn bước đó anh ta trở lại điểm xuất phát. Một người say rượu bước bốn bước. Mỗi bước anh ta tiến lên phía trước nửa mét hoặc lùi lại phía sau nửa mét với xác suất như nhau. Tính xác suất để sau bốn bước đó anh ta trở lại điểm xuất phát. Giải Anh ta trở lại điểm xuất phát khi và chỉ khi trong 4 bước, anh ta có 2 lần bước tiến và 2 lần bước lùi. Dễ thấy có 6 trường hợp để trong 4 bước có 2 tiến, 2 lùi ( {T - T - L - L,T - L - T - L,L - L - T - T, L - T - L - T,T - L - L - T,L - T - T - L}). Mỗi bước tiến hay lùi đều có xác suất là \({1 \over 2}\), nên mỗi trường hợp có xác suất là: \({1 \over 2}.{1 \over 2}.{1 \over 2}.{1 \over 2} = {1 \over {16}}.\) Thành thử xác suất cần tìm là \({6 \over {16}} = {3 \over 8}.\) sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Bài 4, 5: Biến cố và xác suất của biến cố - Các quy tắc tính xác suất
|
-
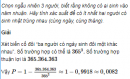
Câu 2.47 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
Chọn ngẫu nhiên 3 người, biết rằng không có ai sinh vào năm nhuận. Hãy tính xác suất để có ít nhất hai người có sinh nhật trùng nhau (cùng ngày, cùng tháng).
-

Câu 2.48 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
Một người đi du lịch mang ba hộp thịt, 2 hộp hoa quả và 3 hộp sữa. Do trời mưa nên các hộp thịt mất nhãn. Người đó chọn ngẫu nhiên ba hộp. Tính xác suất để trong đó có một hộp thịt, một hộp sữa, một hộp hoa quả.
-

Câu 2.49 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
Trong danh sách 10 đường phố cần tu sửa ở Hà Nội, có 2 đường thuộc quận Hoàn Kiếm, 4 đường thuộc quận Ba Đình, 4 đường thuộc quận Đống Đa.
-

Câu 2.50 trang 68 sách bài tập Đại số và Giải tích 11 Nâng cao
Gieo một con súc sắc cân đối ba lần. Gọi X là số lần con súc sắc xuất hiện mặt 6 chấm. a) Lập bảng phân bố xác suất của X.

 Tải ngay
Tải ngay







