Câu 2.68 trang 71 sách bài tập Đại số và Giải tích 11 Nâng caoXác định n để Xác định n để khai triển của \({\left( {x + 2} \right)^n}\) (theo lũy thừa của x), hệ số của số hạng thứ 10 lớn hơn hệ số của số hạng thứ 9 và hệ số của số hạng thứ 11. Giải Khai triển \({\left( {x + 2} \right)^n}\) theo lũy thừa giảm của x là \({\left( {x + 2} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{x^{n - k}}{2^k}} \) Do đó ta phải có \(C_n^9{2^9} > C_n^8{2^8}\) và \(C_n^{9}{2^{9}} > C_n^{10}{2^{10}}\) hay \(2\left( {n - 8} \right) > 0\) và \(10 > 2\left( {n - 9} \right).\) Từ đó 12,5 < n< 14. Suy ra n = 13. sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
Xem thêm tại đây:
Ôn tập chương II - Tổ hợp và xác suất
|
-
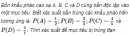
Câu 2.69 trang 71 sách bài tập Đại số và Giải tích 11 Nâng cao
Bốn khẩu pháo cao xạ A, B, C và D cùng bắn độc lập vào một mục tiêu.
-

Câu 2.70 trang 71 sách bài tập Đại số và Giải tích 11 Nâng cao
Một bài kiểm tra trắc nghiệm có 4 câu. Mỗi câu có 5 phương án trả lời trong đó chỉ có một phương án trả lời đúng. Nếu trả lời đúng thì được 5 điểm. Nếu trả lời sai thì không được điểm.
-

Câu 2.71 trang 71 sách bài tập Đại số và Giải tích 11 Nâng cao
Máy bay Boing 747 có 4 động cơ. Xác suất để mỗi động cơ gặp sự cố khi bay là 0,1. Máy bay thực hiện chuyến bay an toàn nếu chỉ có nhiều nhất một trong 4 động cơ gặp sự cố.
-

Câu 2.72 trang 71 sách bài tập Đại số và Giải tích 11 Nâng cao
Số người chết trong một tuần ở vùng A là một biến ngẫu nhiên X có bảng phân bố xác suất như sau:

 Tải ngay
Tải ngay







