Câu 32 trang 24 Sách Bài Tập (SBT) Toán lớp 7 tập 2Tính các giá trị của đa thức. Tính các giá trị của đa thức sau: a) \({\rm{}}xy + {x^2}{y^2} + {x^3}{y^3} + ...+ {x^{10}}{y^{10}}\) tại x = -1; y = 1 b) \(xyz + {x^2}{y^2}{z^2} + {x^3}{y^3}{z^3} + ...+ {x^{10}}{y^{10}}{z^{10}}\) tại x = 1; y = -1; z = -1 Giải a) \({\rm{}}xy + {x^2}{y^2} + {x^3}{y^3} + ... + {x^{10}}{y^{10}}\) \(= xy + {\left( {xy} \right)^2} + {\left( {xy} \right)^3} + ... + {\left( {xy} \right)^{10}}\) Với x = -1 và y = 1 => xy = -1.1 = -1. Thay vào đa thức ta có: \( - 1 + {\left( { - 1} \right)^2} + {\left( { - 1} \right)^3} + ... + {\left( { - 1} \right)^{10}} \) \(= - 1 + 1 + ( - 1) + 1 + ... + ( - 1) + 1 = 0\) b) \(xyz + {x^2}{y^2}{z^2} + {x^3}{y^3}{z^3} + ...+ {x^{10}}{y^{10}}{z^{10}}\) \(= xyz + {\left( {xyz} \right)^2} + {\left( {xyz} \right)^3} + ...+ {\left( {xyz} \right)^{10}}\) Mà với x = 1; y = -1; z = -1 => xyz = 1. (-1). (-1)=1 Thay vào đa thức ta có: \(1 + {1^2} + {1^3} + ... + {1^{10}} = 10\) Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 6: Cộng, trừ đa thức
|
-
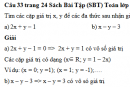
Câu 33 trang 24 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Tìm các cặp giá trị x, y để các đa thức sau nhận giá trị bằng 0.
-
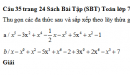
Câu 35 trang 24 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Thu gọn các đa thức sau và sắp xếp theo lũy thừa giảm của biến.

 Tải ngay
Tải ngay







