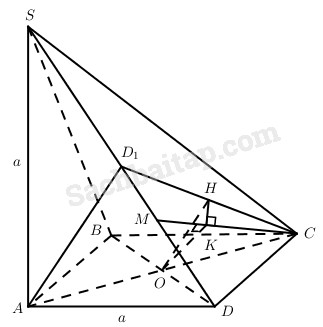
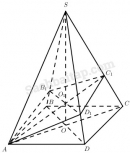
Câu 33 trang 120 Sách bài tập Hình học 11 Nâng caoGiải bài tập Câu 33 trang 120 Sách bài tập Hình học 11 Nâng cao Hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh bên SA vuông góc với mp(ABCD) và SA = a. a) Gọi D1 là trung điểm của SD. Chứng minh rằng \(A{{\rm{D}}_1} \bot \left( {SC{\rm{D}}} \right)\). b) Gọi O là tâm của hình vuông ABCD, M là điểm thay đổi trên SD. Chứng minh rằng hình chiếu của điểm O trên CM thuộc đường tròn cố định. Trả lời
a) Vì SA = AD = a và D1 là trung điểm của SD nên \(A{{\rm{D}}_1} \bot S{\rm{D}}\). Mặt khác, ta có \(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\) nên \(A{{\rm{D}}_1} \bot C{\rm{D}}.\) Vậy \(A{{\rm{D}}_1} \bot \left( {SC{\rm{D}}} \right).\) b) Kẻ OH // AD1 thì H là trung điểm của D1C và \(OH \bot \left( {SC{\rm{D}}} \right)\), ngoài ra H cố định. Gọi K là hình chiếu của O trên CM thì HK ⊥ KC (định lí ba đường vuông góc). Từ đó, suy ra điểm K thuộc đường tròn đường kính HC trong mp(SCD). Đó là đường tròn cố định chứa hình chiếu của tâm hình vuông trên mặt phẳng (SCD). Sachbaitap.com
Xem lời giải SGK - Toán 11 Nâng cao - Xem ngay >> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|
-
Câu 34 trang 120 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 34 trang 120 Sách bài tập Hình học 11 Nâng cao
-
Câu 35 trang 120 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 35 trang 120 Sách bài tập Hình học 11 Nâng cao
-
Câu 36 trang 121 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 36 trang 121 Sách bài tập Hình học 11 Nâng cao
-
Câu 37 trang 121 Sách bài tập Hình học 11 Nâng cao
Giải bài tập Câu 37 trang 121 Sách bài tập Hình học 11 Nâng cao

 Tải ngay
Tải ngay