Câu 3.3 trang 161 Sách bài tập (SBT) Toán 8 tập 1Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC. a. Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC. Chứng minh rằng \({{S'} \over S} = {{DK} \over {AH}}\) b. Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T. Chứng minh rằng \({{MH} \over {AD}} + {{MK} \over {BE}} + {{MT} \over {CF}} = 1\) Giải:
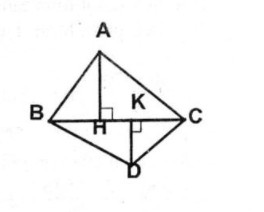
a. Hai ∆ ABC và ∆ DBC có chung canh đáy BC nên ta có: \(\eqalign{ & {S_{ABC}} = {1 \over 2}AH.BC = S \cr & {S_{DBC}} = {1 \over 2}DK.BC = S' \cr} \) Suy ra: \({{S'} \over S} = {{{1 \over 2}DK.BC} \over {{1 \over 2}AH.BC}} = {{DK} \over {AH}}\)
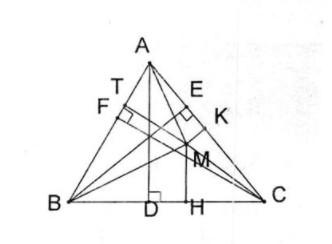
b. Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S1, S2, S3. Ta có: S = S1 +S2 +S3 Trong đó: S = \({1 \over 2}\)AD. BC = \({1 \over 2}\)BE. AC = \({1 \over 2}\)CF . AB \(\eqalign{ & {S_1} = {1 \over 2}MT.AB \cr & {S_2} = {1 \over 2}MK.AC \cr & {S_3} = {1 \over 2}MH.BC \cr & {{{S_1}} \over S} = {{{1 \over 2}MT.AB} \over {{1 \over 2}CF.AB}} = {{MT} \over {CF}} \cr & {{{S_2}} \over S} = {{{1 \over 2}MK.AC} \over {{1 \over 2}BE.AC}} = {{MK} \over {BE}} \cr & {{{S_3}} \over S} = {{{1 \over 2}MH.BC} \over {{1 \over 2}AD.BC}} = {{MH} \over {AD}} \cr & \Rightarrow {{MH} \over {AD}} + {{MK} \over {BE}} + {{MT} \over {CF}} = {{{S_3}} \over S} + {{{S_2}} \over S} + {{{S_1}} \over S} = {{{S_1} + {S_2} + {S_3}} \over S} = {S \over S} = 1 \cr} \)
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 3. Diện tích tam giác
|
-
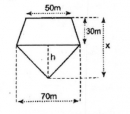
Câu 32 trang 161 Sách bài tập (SBT) Toán 8 tập 1-
Tính x, biết đa giác ở hình 188 có diện tích là 3375 m2.
-
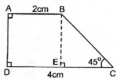
Câu 35 trang 161 Sách bài tập (SBT) Toán 8 tập 1
Tính diện tích của một hình thang vuông, biết hai đáy có độ dài là 2cm và 4cm, góc tạo bởi một cạnh bên và đáy lớn có số đo bằng

 Tải ngay
Tải ngay