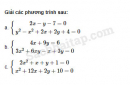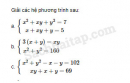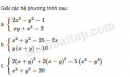Câu 3.49 trang 66 SBT Đại số 10 Nâng caoGiải bài tập Câu 3.49 trang 66 SBT Đại số 10 Nâng cao. Bài toán cổ. Hãy giải bài toán dân gian sau : Em đi chợ phiên Anh gửi một tiền Cam, thanh yên, quýt Không nhiều thì ít Mua đủ một trăm Cam ba đồng một Quýt một đồng trăm Thanh yên tươi tốt Năm đồng một trái Hỏi mỗi thứ mua bao nhiêu trái, biết rằng một tiền là 60 đồng ? Giải: Gọi số cam, quýt, thanh yên lần lượt là x, y, z quả (Điều kiện : x, y, z nguyên dương nhỏ hơn 100) Theo đề bài, ta lập được hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y + {\rm{z}} = 100\,\,\,\,\left( 1 \right)}\\{3{\rm{x}} + \dfrac{y}{5} + 5{\rm{z}} = 60\,\,\,\,\left( 2 \right)}\end{array}} \right.\) Từ (1) và (2) suy ra 7x + 12z = 100 ⇔ 7(x – 16) = -12(z + 1) Vì vậy \(\left\{ {\begin{array}{*{20}{c}}{x - 16 = - 12k}\\{z + 1 = 7k}\end{array}} \right.\left( {k \in Z} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = - 12k + 16}\\{y = 7k - 1}\end{array}} \right.\) Để x, y nguyên dương thì k = 1, Từ đó tìm được x = 4 ; y = 90 ; z = 6 (thỏa mãn điều kiện bài toán). Vậy có 4 quả cam, 90 quả quýt và 6 quả thanh yên. Sachbaitap.com
Xem thêm tại đây:
Bài 4. Phương trình và hệ phương trình bậc nhất nhiều ẩn
|

 Tải ngay
Tải ngay