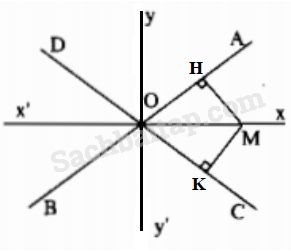
Câu 43 trang 45 Sách Bài Tập (SBT) Toán lớp 7 tập 2Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD. Cho hai đường thẳng AB và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD. Giải
Xét \(M\) nằm trong góc AOC và cách đều OA và OC. Kẻ \(MH \bot OA,MK \bot {\rm{O}}C\) nên MH = MK Xét hai tam giác vuông MHO và MKO: \(\widehat {MHO} = \widehat {MK{\rm{O}}} = 90^\circ \) MH = MK OM cạnh huyền chung Do đó ∆MHO = ∆MKO (cạnh huyền - cạnh góc vuông) \( \Rightarrow \widehat {MOH} = \widehat {MOK}\) (2 góc tương ứng) =>OM là tia phân giác của \(\widehat {AOC}\) Ngược lại, M nằm trên tia phân giác của \(\widehat {AOC}\) Xét hai tam giác vuông MHO và MKO: \(\widehat {MHO} = \widehat {MK{\rm{O}}} = 90^\circ \) \(\widehat {MOH} = \widehat {MOK}\) OM cạnh huyền chung Do đó ∆MHO = ∆MKO (cạnh huyền – góc nhọn) \( \Rightarrow \) MH = MK (2 cạnh tương ứng) Vậy tập hợp các điểm M cách đều OA và OC là tia phân giác Ox của góc AOC. Tương tự M nằm trong các góc AOD, DOB, BOC tập hợp các điểm M là tia phân giác Oy, Ox’, Oy’. Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD. Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 5: Tính chất tia phân giác của một góc
|
-
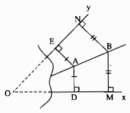
Câu 44 trang 45 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Đường thẳng AB có là đường phân giác của góc xOy hay không.
-
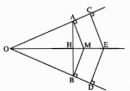
Câu 5.1, 5.2, 5.3, 5.4, 5.5 trang 45, 46 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Hãy chọn phương án đúng.
-
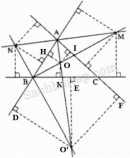
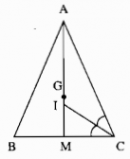
Câu 46 trang 46 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Hãy tìm một điểm sao cho khoảng cách từ điểm đó đến mỗi đoạn thẳng AB, BC, CA là bằng nhau, đồng thời khoảng cách này là ngắn nhất.

 Tải ngay
Tải ngay