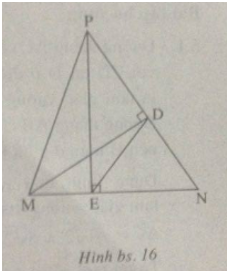
Câu 4.8 trang 117 Sách Bài Tập (SBT) Toán 9 Tập 1Cho tam giác nhọn MNP Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đó kẻ từ M. Chứng minh rằng: a) \({S_{MNP}} = {1 \over 2}MP.NP.\sin P\); b) \(DP = {{MN.\sin N} \over {tgP}}\); c) ∆DNE đồng dạng với ∆MNP, trong đó E là chân đường cao của tam giác MNP kẻ từ P. Gợi ý làm bài
(h.bs. 16) a) Ta có MD = MP sin P, suy ra: \({S_{MNP}} = {1 \over 2}NP.MD = {1 \over 2}NP.MP\sin P.\) b) Ta có MD = MN sin N và MD = DP tg P nên từ đó suy ra DP \( = {{MN\sin N} \over {tgP}}\) c) Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên \({{DN} \over {MN}} = {{EN} \over {PN}}.\) Hai tam giác DNE và MNP đồng dạng vì có góc N chung và \({{DN} \over {MN}} = {{EN} \over {PN}}.\) Sachbaitap.com
Xem lời giải SGK - Toán 9 - Xem ngay >> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 4. Một số hệ thức về cạnh và góc trong tam giác vuông
|
-
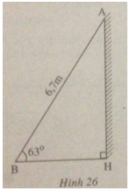
Câu 72 trang 117 Sách Bài Tập (SBT) Toán 9 Tập 1
Thang AB dài 6,7m tựa vào tường làm thành góc 63 với mặt đất (h.26).
-
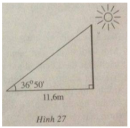
Câu 73 trang 117 Sách Bài Tập (SBT) Toán 9 Tập 1
Làm dây kéo cờ: Tìm chiều dài của dây kéo cờ, biết bóng của cột cờ (chiếu bởi ánh sáng mặt trời) dài 11,6m
-
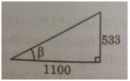
Câu 75 trang 118 Sách Bài Tập (SBT) Toán 9 Tập 1
Đài quan sát ở Toronto, Ontario, Canada cao 533m

 Tải ngay
Tải ngay