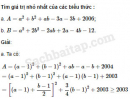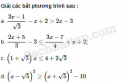Câu 4.85 trang 116 SBT Đại số 10 Nâng caoGiải bài tập Câu 4.85 trang 116 SBT Đại số 10 Nâng cao Cho các số không âm a, b, c. Chứng minh rằng : a. \(\dfrac{{{a^6} + {b^9}}}{4} \ge 3{a^2}{b^3} - 16\) b. \(a + b + 2{a^2} + 2{b^2} \ge 2ab + 2b\sqrt a + 2a\sqrt b .\) Giải: a. Bất đẳng thức cần chứng minh được biến đổi thành : \({a^6} + {b^9} + 64 \ge 12{a^2}{b^3}.\) Áp dụng bất đẳng thức giữa trung bình cộng và trung bình nhân, ta có : \({a^6} + {b^9} + 64 \ge 3\sqrt[3]{{{a^6}{b^9}.64}} = 12{a^2}{b^3}.\) Vậy \({a^6} + {b^9} + 64 \ge 12{a^2}{b^3}\) hay \(\dfrac{{{a^6} + {b^9}}}{4} \ge 3{a^2}{b^3} - 16.\) Đẳng thức xảy ra khi và chỉ khi a = 2, \(b = \sqrt[3]{4}.\) b. Bất đẳng thức cần chứng minh được biến đổi thành : \({\left( {a - b} \right)^2} + {\left( {b - \sqrt a } \right)^2} + {\left( {a - \sqrt b } \right)^2} \ge 0.\) Dấu bằng xảy ra khi và chỉ khi \(a = b = 0\) hoặc \(a = b = 1\). Điều này luôn luôn đúng. Sachbaitap.com
Xem thêm tại đây:
Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
|

 Tải ngay
Tải ngay