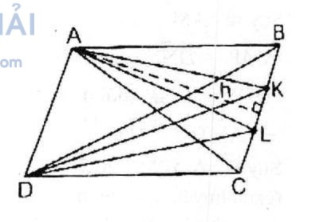
Câu 55 trang 166 Sách bài tập (SBT) Toán 8 tập 1Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC. Tính tỉ số diện tích của : a. Các tam giác DAC và DCK b. Tam giác DAC và tứ giác ADLB c. Các tứ giác ABKD và ABLD Cho hình bình hành ABCD. Gọi K và L là hai điểm thuộc cạnh BC sao cho BK = KL = LC. Tính tỉ số diện tích của : a. Các tam giác DAC và DCK b. Tam giác DAC và tứ giác ADLB c. Các tứ giác ABKD và ABLD Giải:
Ta có: \({S_{ACD}} = {S_{BCD}} = {S_{DAB}} = {S_{CAB}} = {1 \over 2}{S_{ABCD}}\) (1) \(CK = {1 \over 2}CB\) ∆ DCK = ∆ DCB có chung chiều cao kẻ từ đỉnh D, cạnh đáy \(CK = {2 \over 3}CB\) \( \Rightarrow {S_{DCK}} = {2 \over 3}{S_{DBC}}\) (2) Từ (1) và (2) suy ra: \({S_{DCK}} = {2 \over 3}{S_{DAC}} \Rightarrow {{{S_{DCK}}} \over {{S_{DAC}}}} = {2 \over 3}\) b. Ta có: \({S_{ADLB}} = {S_{ADB}} + {S_{DLB}}\) ∆ DBC và ∆ DLC có chung chiều cao kẻ từ đỉnh D, cạnh đáy \(LB = {2 \over 3}BC\) \( \Rightarrow {S_{DLB}} = {2 \over 3}{S_{DBC}}\) mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên) Suy ra: \({S_{ADLB}} = {S_{DAC}} + {2 \over 3}{S_{DAC}} = {5 \over 3}{S_{DAC}} \Rightarrow {{{S_{DAC}}} \over {{S_{ADLB}}}} = {3 \over 5}\) c. Ta có: \({S_{ABKD}} = {S_{ABD}} + {S_{DKB}}\) ∆ DKB và ∆ DCB có chung chiều cao kẻ từ D, cạnh đáy \(BL = {1 \over 3}BC\) \( \Rightarrow {S_{DKB}} = {1 \over 3}{S_{DCB}}\) mà \({S_{DAC}} = {S_{ADB}} = {S_{DBC}}\) (chứng minh trên) \( \Rightarrow {S_{ABKD}} = {S_{DAC}} + {1 \over 3}{S_{DAC}} = {4 \over 3}{S_{DAC}} \Rightarrow {{{S_{ABKD}}} \over {{S_{ADLB}}}} = {{{4 \over 3}{S_{DAC}}} \over {{5 \over 3}{S_{DAC}}}} = {4 \over 5}\)
Xem lời giải SGK - Toán 8 - Xem ngay >> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Ôn tập chương II - Đa giác - Diện tích đa giác
|
-
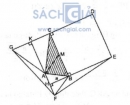
Câu 56 trang 166 Sách bài tập (SBT) Toán 8 tập 1
Cho tam giác ABC vuông ở A và có BC = 2 AB = 2a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều ACG.

 Tải ngay
Tải ngay