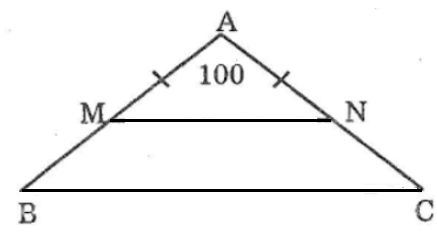
Câu 68 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1Chứng minh rằng MN // BC. Cho tam giác ABC cân tại A có \(\widehat A = 100^\circ\). Lấy điểm M thuộc cạnh AB, điểm N thuộc cạnh AC sao cho AM = AN. Chứng minh rằng MN // BC. Giải
Vì ∆ABC cân tại A nên \(\widehat B = \widehat C\) Áp dụng định lí tổng 3 góc trong một tam giác ta có: \(\begin{gathered} \(\widehat B = \dfrac{{{{180}^\circ } - \widehat A}}{2}\) \( \;\;\;\;= \dfrac{{{{180}^\circ } - {{100}^\circ }}}{2} = {40^\circ } \) (1) Mà AM = AN (gt) nên ∆AMN cân tại A \(\Rightarrow \widehat {AMN} = \widehat {ANM}\) Áp dụng định lí tổng 3 góc trong một tam giác ta có: \(\begin{gathered} \(\Rightarrow \widehat {AMN} = \dfrac{{{{180}^\circ } - \widehat A}}{2} = \dfrac{{{{180}^\circ } - {{100}^\circ }}}{2}\)\(\, = {40^\circ } \) (2) Từ (1) và (2) suy ra: \(\widehat B = \widehat {AMN}=40^o\) Vậy MN // BC (vì có cặp góc ở vị trí đồng vị bằng nhau). Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 6: Tam giác cân
|
-
Câu 71 trang 147 Sách Bài Tập (SBT) Toán lớp 7 tập 1
Vẽ lại hình 59 vào vở rồi đặt bài toán vẽ tam giác để có hình 59.

 Tải ngay
Tải ngay