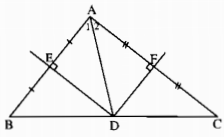
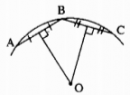
Câu 7.4, 7.5, 7.6 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2Chứng minh rằng: a) D là trung điểm của cạnh BC. Câu 7.4 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2 Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng: a) D là trung điểm của cạnh BC. b) \(\widehat A = \widehat B + \widehat C\) Giải
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC. b) Ta có ∆DEB = ∆DEA(c.g.c) nên \(\widehat B = \widehat {{A_1}}\). Tương tự \(\widehat C = \widehat {{A_2}}\). Suy ra \(\widehat A = \widehat {{A_1}} + \widehat {{A_2}} = \widehat B + \widehat C\) Câu 7.5 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2 Chứng minh rằng nếu trong tam giác ABC có hai cạnh AB và AC không bằng nhau thì đường trung tuyến xuất phát từ đỉnh A không vuông góc với BC. Giải
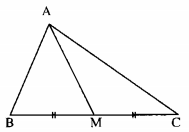
Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của cạnh BC. Giả sử \(AM \bot BC\). Khi đó AM là đường trung trực của đoạn thẳng BC. Suy ra AB = AC. Điều này mâu thuẫn với giả thiết AB không bằng AC. Vậy trung tuyến AM không vuông góc với BC. Câu 7.6 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2 Cho đường thẳng d và hai điểm A, B nằm về một phía của d sao cho AB không vuông góc với d. Hãy tìm trên d một điểm M sao cho \(\left| {MA - MB} \right|\) có giá trị nhỏ nhất. Giải
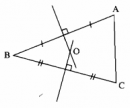
Ta có \(\left| {MA - MB} \right| \ge 0\) với một điểm M tùy ý và \(\left| {MA - MB} \right| = 0\) chỉ với các điểm M mà MA = MB, tức là chỉ với các điểm M nằm trên đường trung trực của đoạn thẳng AB. Mặt khác M phải thuộc d. Vậy M là giao điểm của đường thẳng d và đường trung trực của đoạn thẳng AB. Có giao điểm này vì AB không vuông góc với d. Tóm lại: Khi M là giao điểm của d và đường trung trực của đoạn thẳng AB thì \(\left| {MA - MB} \right|\) đạt giá trị nhỏ nhất và bằng 0. Sachbaitap.com
Xem lời giải SGK - Toán 7 - Xem ngay >> Học trực tuyến lớp 7 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
Xem thêm tại đây:
Bài 7: Tính chất đường trung trực của một đoạn thẳng
|
-
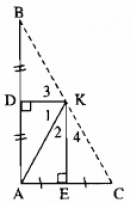
Câu 66 trang 49 Sách Bài Tập (SBT) Toán lớp 7 tập 2
Chứng minh rằng: a) Các đường trung trực của tam giác vuông đi qua trung điểm của cạnh huyền.

 Tải ngay
Tải ngay